Предмет: Математика,
автор: VLAD999
Вычислите неопределенный интеграл.
Приложения:
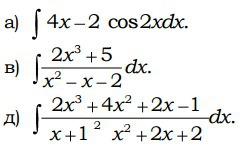
Ответы
Автор ответа:
0
a
2x²-sin2x+C
б
Выделим целую часть из дроби
2x³+5 | x²-x-2
2x³-2x²-4x 2x+2
-----------------
2x²+4x+5
2x²-2x-4
---------------
6x+9
Дробную часть представим как сумму дробей
x²-x-2=(x-2)(x+1)
x1+x2=1 U x1*x2=-2
(6x+9)/(x-2)(x+1)=A/(x-2)+B/(x+1)
Ax+A+Bx-2B=6x+9
(A+B)x +(A-2B)=6x+9
{A+B=6⇒A=6-B
{A-2B=9
6-B-2B= 9
3B=-3
B=-1
A=7
Получили под интегралом
(2x³+5)/(x²-x-2)=(2x+2)+7/(x-2)-1/(x+1)


3
Сделаем преобразования подинтегральной функции
(2x³+4x²+2x-1)/[(x+1)²(x²+2x+2)]=(2x+1)/(x²+2x+2)-1/(x+1)²=
(2x+2)/(x²+2x+2)-1/(2x+2x+2)-1/(x+1)²=
=(x²+2x+2)`/(x²+2x+2)-1/[(x+1)²+1]-1/(x+1)²
![intlimits {(x^2+2x+2)`/(x^2+2x+2)} , dx - intlimits {1/[(x+1)^2+1]} , dx - intlimits {(x^2+2x+2)`/(x^2+2x+2)} , dx - intlimits {1/[(x+1)^2+1]} , dx -](https://tex.z-dn.net/?f=+intlimits+%7B%28x%5E2%2B2x%2B2%29%60%2F%28x%5E2%2B2x%2B2%29%7D+%2C+dx+-+intlimits+%7B1%2F%5B%28x%2B1%29%5E2%2B1%5D%7D+%2C+dx+-)

2x²-sin2x+C
б
Выделим целую часть из дроби
2x³+5 | x²-x-2
2x³-2x²-4x 2x+2
-----------------
2x²+4x+5
2x²-2x-4
---------------
6x+9
Дробную часть представим как сумму дробей
x²-x-2=(x-2)(x+1)
x1+x2=1 U x1*x2=-2
(6x+9)/(x-2)(x+1)=A/(x-2)+B/(x+1)
Ax+A+Bx-2B=6x+9
(A+B)x +(A-2B)=6x+9
{A+B=6⇒A=6-B
{A-2B=9
6-B-2B= 9
3B=-3
B=-1
A=7
Получили под интегралом
(2x³+5)/(x²-x-2)=(2x+2)+7/(x-2)-1/(x+1)
3
Сделаем преобразования подинтегральной функции
(2x³+4x²+2x-1)/[(x+1)²(x²+2x+2)]=(2x+1)/(x²+2x+2)-1/(x+1)²=
(2x+2)/(x²+2x+2)-1/(2x+2x+2)-1/(x+1)²=
=(x²+2x+2)`/(x²+2x+2)-1/[(x+1)²+1]-1/(x+1)²
Похожие вопросы
Предмет: История,
автор: 20mila6ka08
Предмет: Английский язык,
автор: chachatryanariana
Предмет: Геометрия,
автор: madina2629
Предмет: Математика,
автор: bulatnikovamas
Предмет: Литература,
автор: vanchatzedemyanenko