Question

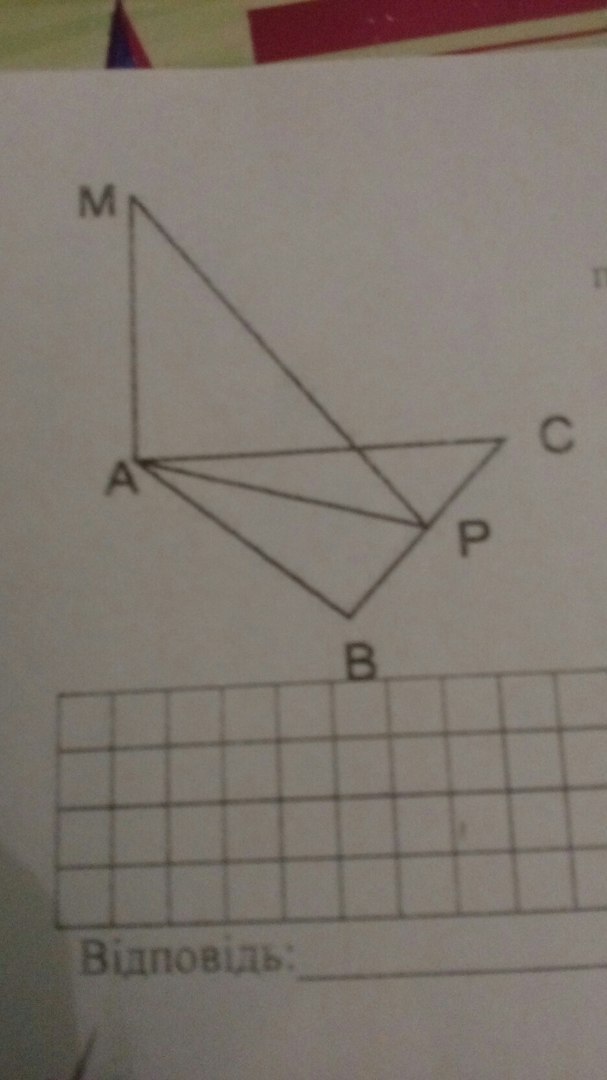
В правильном треугольнике ABC со стороной AB = 4 см, через вершину A проведено перпендикуляр АМ к плоскости треугольника ABC, AM = 4√3 см.
А) Докажите, что прямая BC перпендикулярна
плоскости AMP, где P - середина стороны BC.
Б) Найдите расстояние от точки M до прямой BC

Answer 1

ABC - равносторонний, где AP - высота, медиана, биссектриса. ⇒ AP ⊥ BC. Плоскость перпендикулярна, если прямая, лежащая в плости, перпендикулярна, а раз AP ⊥ BC, то плоскость AMP ⊥ BC

Высота в равностороннем треугольнике - $frac{a sqrt{3} }{2}$
a = 4. Высота, AP, равна 2√3. Рассмотрим треугольник MAP, MA ⊥ AP - треугольник прямоугольный. MP² = MA² + AP² по теореме Пифагора
MP² = 60. MP = 4√15