Предмет: Математика,
автор: golotina25l
пожалуйста,срочно решите 1 вариант
Приложения:
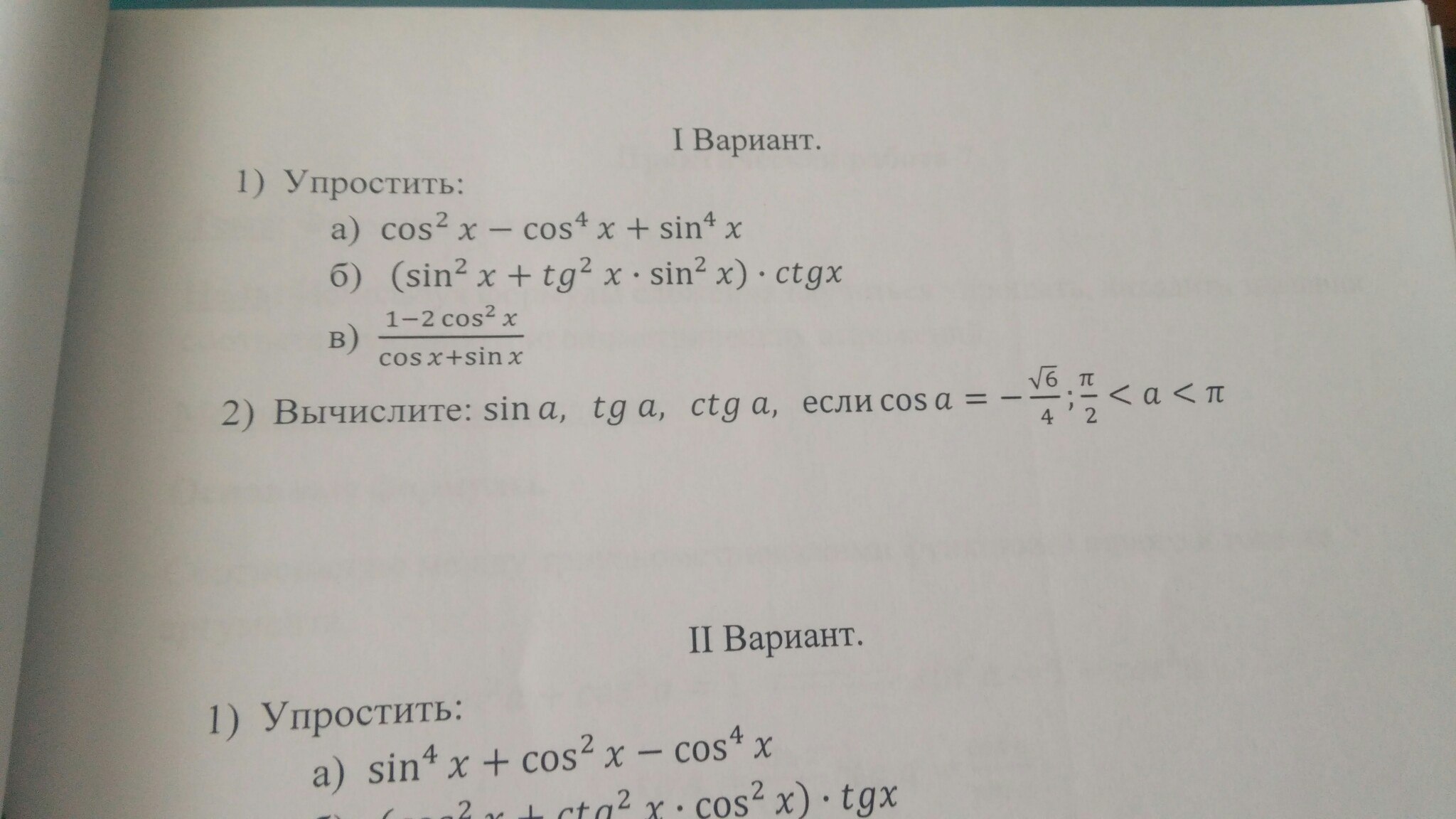
Ответы
Автор ответа:
0
№1
а)Cos²x(1 - Cos²x) + Sin⁴x = Cos²x*Sin²x + Sin⁴x = Sin²x(Cos²x + Sin²x) =
=Sin²x
б) Sin²x(1 + tg²x) *Ctgx = Sin²x * 1/Cos²x * Ctgx = tg²x * Ctgx = tgx
в) числитель = 1 - 2Cos²x = Sin²x + Cos²x -2Cos²x = Sin²x - Cos²x =
=(Sinx - Cosx)(Sinx + Cosx)
теперь видно, что дробь сокращается.
Ответ: Sinx - Cosx
№2
Cosα = -√6/4
α∈ 2 четв.
Sinα = √(1 - 6/16)= √10/16 = √10/4
tgα = Sinα/Cosα = -√10/√6 = -√5/√3 = -√15/3
Ctgα = -3/√15 = -√15/5
а)Cos²x(1 - Cos²x) + Sin⁴x = Cos²x*Sin²x + Sin⁴x = Sin²x(Cos²x + Sin²x) =
=Sin²x
б) Sin²x(1 + tg²x) *Ctgx = Sin²x * 1/Cos²x * Ctgx = tg²x * Ctgx = tgx
в) числитель = 1 - 2Cos²x = Sin²x + Cos²x -2Cos²x = Sin²x - Cos²x =
=(Sinx - Cosx)(Sinx + Cosx)
теперь видно, что дробь сокращается.
Ответ: Sinx - Cosx
№2
Cosα = -√6/4
α∈ 2 четв.
Sinα = √(1 - 6/16)= √10/16 = √10/4
tgα = Sinα/Cosα = -√10/√6 = -√5/√3 = -√15/3
Ctgα = -3/√15 = -√15/5
Похожие вопросы
Предмет: Математика,
автор: School35788
Предмет: Русский язык,
автор: artemyakovlev1111
Предмет: Математика,
автор: ma6a1994p728ka
Предмет: Литература,
автор: eryominzhenyok
Предмет: Обществознание,
автор: Настя23062000