Предмет: Математика,
автор: alnasaver
Вычислить определённый интеграл! Помогите!
Приложения:
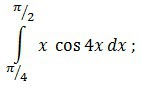
Ответы
Автор ответа:
0
Так как представлен интеграл от произведения функций, то используется метод интегрирования по частям:
u=x ⇒ du=dx
dv=cos4xdx ⇒
Похожие вопросы
Предмет: География,
автор: TIRAI
Предмет: Математика,
автор: mamincheburek99
Предмет: Математика,
автор: goncarovatetana3
Предмет: Математика,
автор: yanysitacom
Предмет: История,
автор: nizamovagulnaz3