Предмет: Математика,
автор: Greenunicorn12
Показательные уравнения!! Помогите!
Приложения:
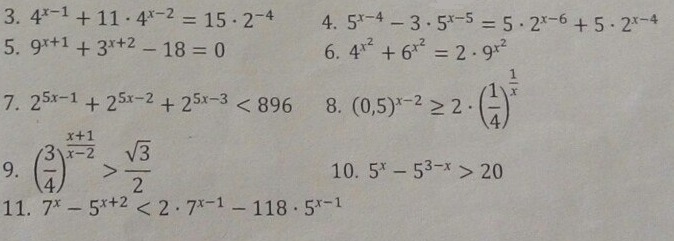
Ответы
Автор ответа:
0
3) 4ˣ⁻²(4 + 11) = 15 *1/16
4ˣ⁻² *15 = 15* 1/16
4ˣ⁻² = 1/16
4ˣ⁻² = 4⁻²
х -2 = -2
х = 0
4) 5 ˣ⁻⁵(5 - 3) = 2ˣ⁻⁶(5 + 5*2²)
5ˣ⁻⁵ *2 = 2ˣ⁻⁶ *25 |:50
5ˣ⁻⁷ = 2ˣ⁻⁷ |: 2ˣ⁻⁷
(5/2)ˣ⁻⁷ = 1
х -7 = 0
х = 7
5) 9ˣ*9 + 3ˣ*3² -18 = 0 |:9
9ˣ + 3ˣ -2 = 0
3ˣ= у
у² +у -2 = 0
по т. Виета у₁ = -2 у₂ = 1
а)3ˣ = -2
нет решений
б)3ˣ = 1
х = 0
6) 2²ˣ² + (2*3)ˣ² = 2*3²ˣ² |: 3²ˣ²
(2/3)²ˣ² + (2/3)ˣ² = 2
(2/3)ˣ² = у
у² +у -2 = 0
По т. Виета у₁ = -2, у₂ = 1
а)(2/3)ˣ² = -2
нет решений
б)(2/3)ˣ² = 1
х² = 0
х = 0
7)2⁵ˣ⁻³(5² + 2 + 1) < 896
2⁵ˣ⁻³ * 28 < 896
2⁵ˣ⁻³ < 32
2⁵ˣ⁻³ < 2⁵
5x -3 < 5
5x < 8
x < 1,6
8)(0,5)ˣ⁻² ≥ 2* (0,5)²/ˣ
(0,5)ˣ⁻³ ≥(0,5)²/ˣ
x - 3 ≤ 2/х
х - 3 - 2/х ≤ 0
(х² -3х -2)/х ≤ 0
метод интервалов
х² - 3х -2 = 0
корни 1 и 2 ( это нули числителя)
х=0 ( это нуль знаменателя)
-∞ 0 1 2 +∞
+ + - + это знаки числителя
- + + + это знаки знаменателя
IIIIIIIIIIII IIIIIIIIIII это решение неравенства
х∈(-∞; 0)∪[1; 2]
9) (√3/2)²*ˣ⁺¹/ˣ⁻² > √3/2
2*(х +1)/(х -2) <1
метод интервалов
2*(х +1)/(х -2) - 1<0
(2x +2 - x +2)/(х -2) < 0
x +4 = 0
x = - 4 (это нуль числителя)
x -2 = 0
x = 2 ( это нуль знаменателя)
-∞ -4 2 +∞
+ - + это знаки дроби
Ответ: х∈ (-4; 2)
10) 5ˣ - 5³⁻ˣ > 20 |*5ˣ
(5ˣ)² -125 > 20*5ˣ
5ˣ = y
y² -20y -125 > 0
по т. Виета корни -5 и 25
решение у > -5 и у < 25
5ˣ < 25
x < 2
11) 7ˣ - 2*7ˣ⁻¹ < 5ˣ⁺² - 118*5ˣ⁻¹
7ˣ⁻¹(7 - 2) < 5ˣ⁻¹(125 -118)
7ˣ⁻¹*5 < 5ˣ⁻¹ *7 | :5*7
7ˣ⁻² < 5ˣ⁻² |: 5ˣ⁻²
(7/5)ˣ⁻² < 1
x - 2 < 0
x < 2
4ˣ⁻² *15 = 15* 1/16
4ˣ⁻² = 1/16
4ˣ⁻² = 4⁻²
х -2 = -2
х = 0
4) 5 ˣ⁻⁵(5 - 3) = 2ˣ⁻⁶(5 + 5*2²)
5ˣ⁻⁵ *2 = 2ˣ⁻⁶ *25 |:50
5ˣ⁻⁷ = 2ˣ⁻⁷ |: 2ˣ⁻⁷
(5/2)ˣ⁻⁷ = 1
х -7 = 0
х = 7
5) 9ˣ*9 + 3ˣ*3² -18 = 0 |:9
9ˣ + 3ˣ -2 = 0
3ˣ= у
у² +у -2 = 0
по т. Виета у₁ = -2 у₂ = 1
а)3ˣ = -2
нет решений
б)3ˣ = 1
х = 0
6) 2²ˣ² + (2*3)ˣ² = 2*3²ˣ² |: 3²ˣ²
(2/3)²ˣ² + (2/3)ˣ² = 2
(2/3)ˣ² = у
у² +у -2 = 0
По т. Виета у₁ = -2, у₂ = 1
а)(2/3)ˣ² = -2
нет решений
б)(2/3)ˣ² = 1
х² = 0
х = 0
7)2⁵ˣ⁻³(5² + 2 + 1) < 896
2⁵ˣ⁻³ * 28 < 896
2⁵ˣ⁻³ < 32
2⁵ˣ⁻³ < 2⁵
5x -3 < 5
5x < 8
x < 1,6
8)(0,5)ˣ⁻² ≥ 2* (0,5)²/ˣ
(0,5)ˣ⁻³ ≥(0,5)²/ˣ
x - 3 ≤ 2/х
х - 3 - 2/х ≤ 0
(х² -3х -2)/х ≤ 0
метод интервалов
х² - 3х -2 = 0
корни 1 и 2 ( это нули числителя)
х=0 ( это нуль знаменателя)
-∞ 0 1 2 +∞
+ + - + это знаки числителя
- + + + это знаки знаменателя
IIIIIIIIIIII IIIIIIIIIII это решение неравенства
х∈(-∞; 0)∪[1; 2]
9) (√3/2)²*ˣ⁺¹/ˣ⁻² > √3/2
2*(х +1)/(х -2) <1
метод интервалов
2*(х +1)/(х -2) - 1<0
(2x +2 - x +2)/(х -2) < 0
x +4 = 0
x = - 4 (это нуль числителя)
x -2 = 0
x = 2 ( это нуль знаменателя)
-∞ -4 2 +∞
+ - + это знаки дроби
Ответ: х∈ (-4; 2)
10) 5ˣ - 5³⁻ˣ > 20 |*5ˣ
(5ˣ)² -125 > 20*5ˣ
5ˣ = y
y² -20y -125 > 0
по т. Виета корни -5 и 25
решение у > -5 и у < 25
5ˣ < 25
x < 2
11) 7ˣ - 2*7ˣ⁻¹ < 5ˣ⁺² - 118*5ˣ⁻¹
7ˣ⁻¹(7 - 2) < 5ˣ⁻¹(125 -118)
7ˣ⁻¹*5 < 5ˣ⁻¹ *7 | :5*7
7ˣ⁻² < 5ˣ⁻² |: 5ˣ⁻²
(7/5)ˣ⁻² < 1
x - 2 < 0
x < 2
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: timur66661
Предмет: Физика,
автор: dbondar743
Предмет: Литература,
автор: elenkachurikov
Предмет: Физика,
автор: KislInKa050501