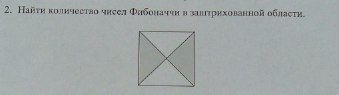
Числа Фибоначчи, совершенные числа, нужна помощь.

Ответы
Суть первого задания мне непонятна. А вот по поводу второго могу предложить такой вариант решения:
Сначала немного о совершенных числах.
Совершенное число — натуральное число, равное сумме всех своих собственных делителей (то есть всех положительных делителей, отличных от
самого́ числа).
Например, делителями числа 6 являются: 1, 2 и
3. Их сумма =6 (1+2+3=6). Следовательно число 6 совершенно.
Таких чисел известно не так много и они
представляют определенную последовательность:
6,
28,
496,
8128,
33 550 336,
8 589 869 056,
137 438 691 328,
2 305 843 008 139 952 128,
2 658 455 991 569 831 744 654 692 615 953 842 176,
В нашем задании думаю можно ограничиться первыми четырьмя числами, т.к.
вряд ли будет рассматриваться массив из более чем 10000 элементов.
1-е совершенное число — 6 имеет следующие собственные делители: 1, 2, 3; их сумма равна 6.
Т.о. Решением задачи будет выражение:
Rez = A[1] * A[2] * A[3] Где: A – массив элементов, A[i] – элемент массива А
2-е совершенное число — 28 имеет следующие
собственные делители: 1, 2, 4, 7, 14; их сумма равна 28.
Т.о. решением задачи также будет выражение:
Rez = A[1] * A[2] * A[4] * A[7] * A[14]
3-е совершенное число — 496 имеет следующие
собственные делители: 1, 2, 4, 8, 16, 31, 62, 124, 248; их сумма равна 496.
Т.о. решением задачи также будет выражение:
Rez = A[1] * A[2] * A[4] * A[8] * A[16] * A[31] * A[62] * A[124] * A[248]
4-е совершенное число — 8128 имеет следующие
собственные делители: 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064;
их сумма равна 8128.
Т.о. решением задачи также будет выражение:
Rez = A[1] * A[2] * A[4] * A[8] * A[16] * A[32] * A[64] * A[127] * A[254] * A[508] * A[1016] * A[2032] * A[4064]