Question

из вершины С тупого угла ромба проведены высоты СМ и СN . Известно, что МN= СМ. Найти углы ромба.

Answer 1

CM=CN U CM=MN⇒ΔCMN-равноберенный⇒<CMN=<CNM=<MCN=60
<BMC=<DNC=90
<NMA=<MNA=180-(<BMC+<CMN)=180-(90+60)=30
<A=180-2<NMA=180-60=120
<A+<B=180⇒<B=180-120=60
<A=<C U <B=<D

Answer 2

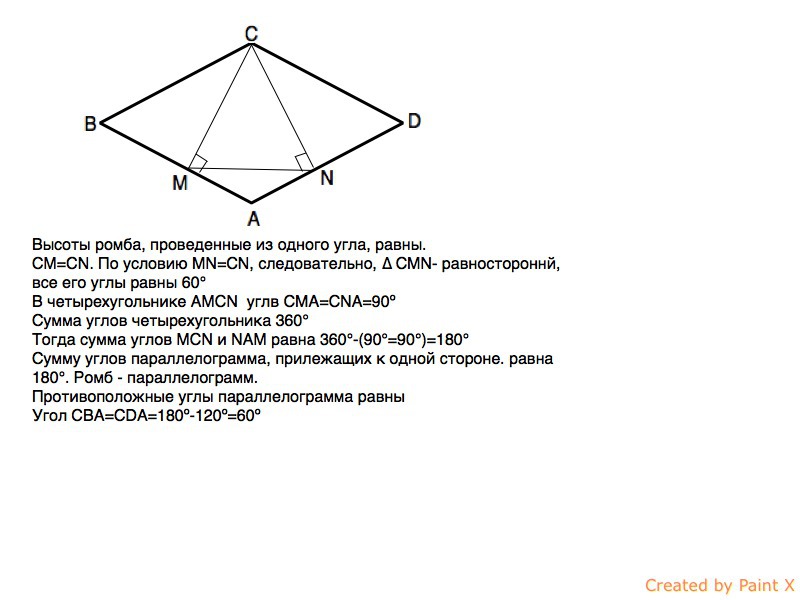
Вариант ответа.

Высоты ромба, проведенные из одного угла, равны. 

СМ=CN. По условию MN=CN, следовательно, ∆ CMN- равносторонний, все его углы равны 60°

В четырехугольнике AMCN  ∠СМА=∠CNA=90º

Сумма углов четырехугольника 360°

Тогда сумма углов MCN и NAM равна 360°-(90°+90°)=180°

∠MAN=180º-60º=120º

Сумма углов параллелограмма, прилежащих к одной стороне. равна 180°. Ромб - параллелограмм.

Противоположные углы параллелограмма равны 

Угол СВА=СDA=180º-120º=60º

∠BAD=∠DAB=120º