Предмет: Математика,
автор: sugarflower
Решите уравнение плиз
Приложения:
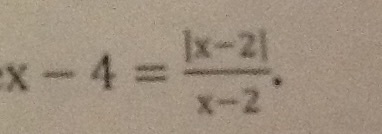
Ответы
Автор ответа:
0
Для каждого выражения под модулем в ур-нии
допускаем случаи, когда соотв. выражение ">= 0" или "< 0",
решаем получившиеся ур-ния.
1.
x−2≥0x−2≥0или
2≤x∧x<∞2≤x∧x<∞получаем ур-ние
x−1−4=0x−1−4=0упрощаем, получаем
x−5=0x−5=0решение на этом интервале:
x1=5x1=5
2.
x−2<0x−2<0или
−∞<x∧x<2−∞<x∧x<2получаем ур-ние
x−−x+2x−2−4=0x−−x+2x−2−4=0упрощаем, получаем
x−−x+2x−2−4=0x−−x+2x−2−4=0решение на этом интервале:
x2=3x2=3
но x2 не удовлетворяет неравенству
Тогда, окончательный ответ:
x1=5
допускаем случаи, когда соотв. выражение ">= 0" или "< 0",
решаем получившиеся ур-ния.
1.
x−2≥0x−2≥0или
2≤x∧x<∞2≤x∧x<∞получаем ур-ние
x−1−4=0x−1−4=0упрощаем, получаем
x−5=0x−5=0решение на этом интервале:
x1=5x1=5
2.
x−2<0x−2<0или
−∞<x∧x<2−∞<x∧x<2получаем ур-ние
x−−x+2x−2−4=0x−−x+2x−2−4=0упрощаем, получаем
x−−x+2x−2−4=0x−−x+2x−2−4=0решение на этом интервале:
x2=3x2=3
но x2 не удовлетворяет неравенству
Тогда, окончательный ответ:
x1=5
Похожие вопросы
Предмет: Математика,
автор: ivanchik1599
Предмет: Русский язык,
автор: Drezzar
Предмет: Математика,
автор: Ekaterinasvi14
Предмет: Математика,
автор: Аноним