Question

Среди чисел х и у, удовлетворяющих одновременно неравенствам х-у больше или равно 1,х+2у больше или равно 2, х+у меньше 3 найти min x и max y

Answer 1

x-y≥1         -y≥1-x       y≤x-1
x+2y≥2      2y≥2-x      y≥1-x/2
x+y<3        y<3-x        y<3-x
Получили три прямые:
в первом уравнении - все точки прямой y=x-1 и ниже её
во втором уравнении  - все точки прямой y=1-x/2 и выше её
в третье уравнении - все точки ниже прямой y=3-x
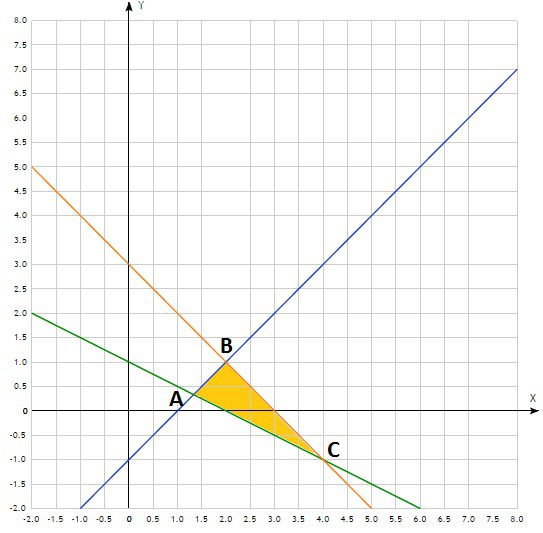
На пересечении прямых находим вершины получившегося треугольника. Обозначим их АВС.
А: x-1=1-x/2
    x+x/2=1+1
   3x/2=2
   x=4/3       y=4/3-1=1/3     A(4/3;1/3)

B: x-1=3-x
    x+x=3+1
    2x=4
    x=2         y=2-1=1          B(2;1)

C: 1-x/2=3-x
     x-x/2=3-1
     x/2=2
     x=4        y=1-4/2=-1      C(4;-1)

min x=4/3      max y→1 (стемится к 1 так как 1 не входит в область значений по условию: х+у<3)
(если бы было x+y≤3, то max y=1)