Предмет: Алгебра,
автор: Stillinski
y=x^2+1/x
Помогите плизз или объясните хотя-бы
Задание Исследовать функцию и построить график
1.Признаки возрастания и убывания
2.Экстремумы функции.Условия существования экстремумы в функции точки
3.Вогнутость и выпуклость кривой
4.Виды асимптот и методы их нахождения
5.Общая схема исследования
Ответы
Автор ответа:
0
Давай по твоим вопросам проедемся , а потом проведём полностью исследование и построим график.
1) чтобы понять: функция возрастает или убывает, надо возиться с производной. Производную приравнивают к нулю, решают уравнение ( корни этого уравнения - это критические точки. они могут точками экстремума . Если производная меняет свой знак при переходе через критическую точку с "+" на "-", значит, эта точка - точка максимума. Слева от этой точки функция возрастает ( график "лезет" вверх) , а справа убывает( график "едет" вниз)
2) асимптоты. разберёмся по ходу дела.
А теперь начали.
Исследование:
у = (х² +1)/х
1)область определения: х ≠ 0 ( уже понятно, что график будет разорван, т.к. х = 0 брать нельзя, а другие значения х ( положительные и отрицательные) - можно. Сразу: х = 0 это асимптота
2)производную ищем по формуле (U/V)' =(U'V - UV')/V²
у' = (2x*x - (x²+1)*1)/х² = (х² -1)/х²
3) Ищем критические точки:
(х² -1)/х²= 0 , ⇒ х² -1 = 0 и х≠0,⇒ х = +-1 и х ≠0
Смотрим знак производной на числовой прямой
-∞ -1 0 1 +∞
+ - - +
max min
y₋₁ = -2; у₀ не существует; у₁ = 2
Итак, нашлись точки графика(-1;-2) и (1;2)
4) Ищем характеристические точки ( это точки пересечения графика данной функции с осями)
а) с осью х ( если точка на оси х, то её координата по оси у = 0)
у = (х² +1)/х
(х² +1)/х= 0
∅
вывод: график с осью х не пересекается)
б) с осью у( если точка на оси у, то её координата по оси х = 0)
у = (х² +1)/х
∅
вывод: график с осью у не пересекается.
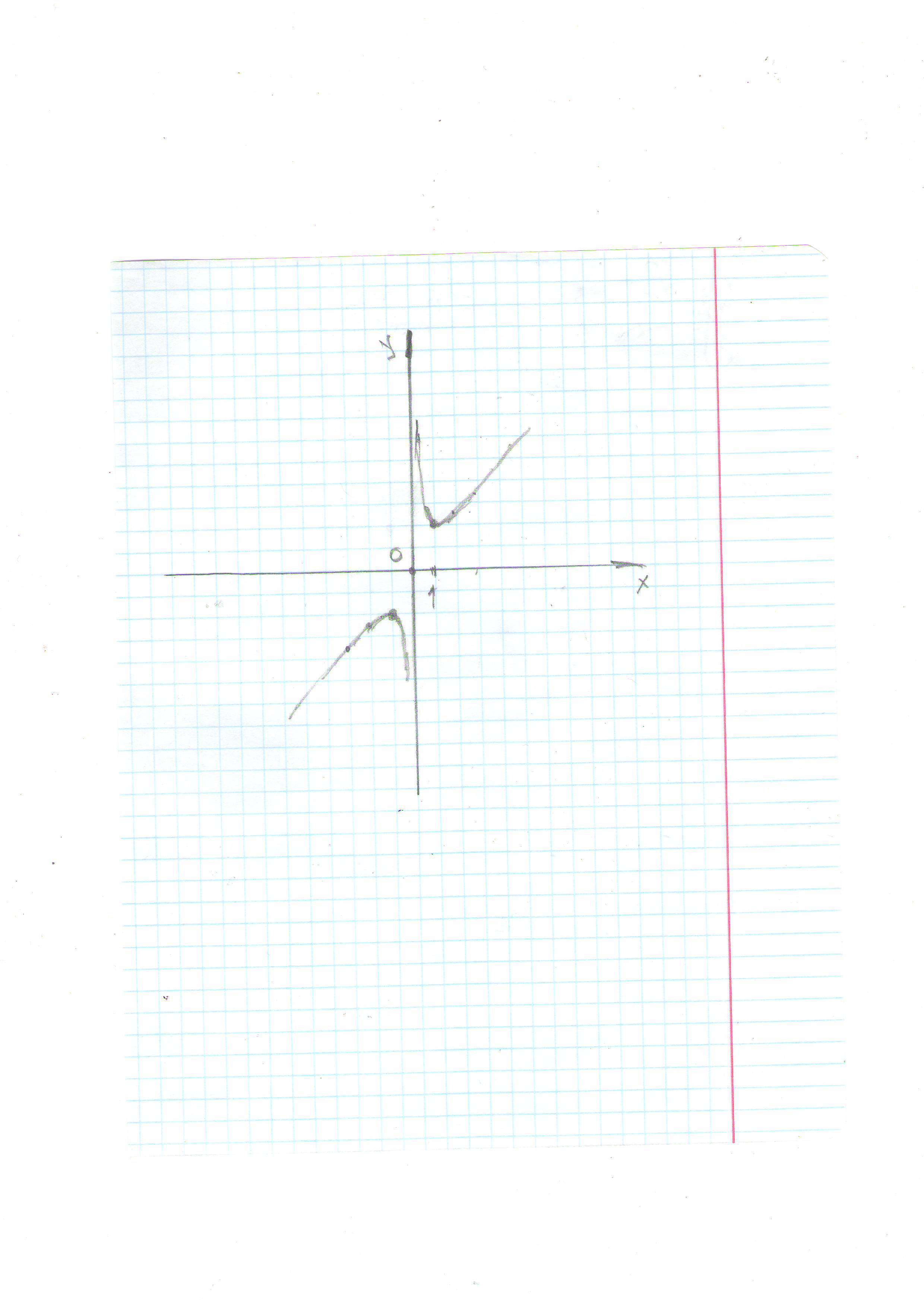
5) можно строить график.
1) чтобы понять: функция возрастает или убывает, надо возиться с производной. Производную приравнивают к нулю, решают уравнение ( корни этого уравнения - это критические точки. они могут точками экстремума . Если производная меняет свой знак при переходе через критическую точку с "+" на "-", значит, эта точка - точка максимума. Слева от этой точки функция возрастает ( график "лезет" вверх) , а справа убывает( график "едет" вниз)
2) асимптоты. разберёмся по ходу дела.
А теперь начали.
Исследование:
у = (х² +1)/х
1)область определения: х ≠ 0 ( уже понятно, что график будет разорван, т.к. х = 0 брать нельзя, а другие значения х ( положительные и отрицательные) - можно. Сразу: х = 0 это асимптота
2)производную ищем по формуле (U/V)' =(U'V - UV')/V²
у' = (2x*x - (x²+1)*1)/х² = (х² -1)/х²
3) Ищем критические точки:
(х² -1)/х²= 0 , ⇒ х² -1 = 0 и х≠0,⇒ х = +-1 и х ≠0
Смотрим знак производной на числовой прямой
-∞ -1 0 1 +∞
+ - - +
max min
y₋₁ = -2; у₀ не существует; у₁ = 2
Итак, нашлись точки графика(-1;-2) и (1;2)
4) Ищем характеристические точки ( это точки пересечения графика данной функции с осями)
а) с осью х ( если точка на оси х, то её координата по оси у = 0)
у = (х² +1)/х
(х² +1)/х= 0
∅
вывод: график с осью х не пересекается)
б) с осью у( если точка на оси у, то её координата по оси х = 0)
у = (х² +1)/х
∅
вывод: график с осью у не пересекается.
5) можно строить график.
Приложения:
Автор ответа:
0
Спасибо большое
Похожие вопросы
Предмет: Алгебра,
автор: vFlower
Предмет: Беларуская мова,
автор: lysenkovlad63
Предмет: Русский язык,
автор: dvdimas228
Предмет: Алгебра,
автор: bagi801