Question

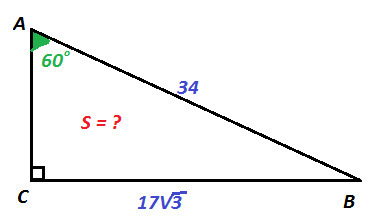
В прямоугольном треугольнике один из катетов равен 17 кв корень из 3, угол, лежащий напротив него равен 60 градусам, а гипотенуза равна 34 .Найдите площадь треугольника. напишите решение плиз,очень надо

Answer 1

ΔABC - прямоугольный, ∠С = 90°, ∠А = 60°, BC = 17√3; AB = 34

Сумма острых углов прямоугольного треугольника равна 90°.  ⇒

∠B = 90° - ∠A = 90° - 60° = 30°

Катет, лежащий напротив угла 30°, равен половине гипотенузы. ⇒

AC = AB : 2 = 34 : 2 = 17

Площадь прямоугольного треугольника равна половине произведения катетов.

$S = \dfrac {AC\cdot BC}{2}=\dfrac{17\cdot 17\sqrt3}{2}=144,5\sqrt 3$

Ответ : 144,5√3  ≈   250,28 кв. ед.