Предмет: Алгебра,
автор: meme9
Вычислите пределы функций, нужно срочно . Пожалуйста помогите кто-нибудь. Дам хороший балл.
Приложения:
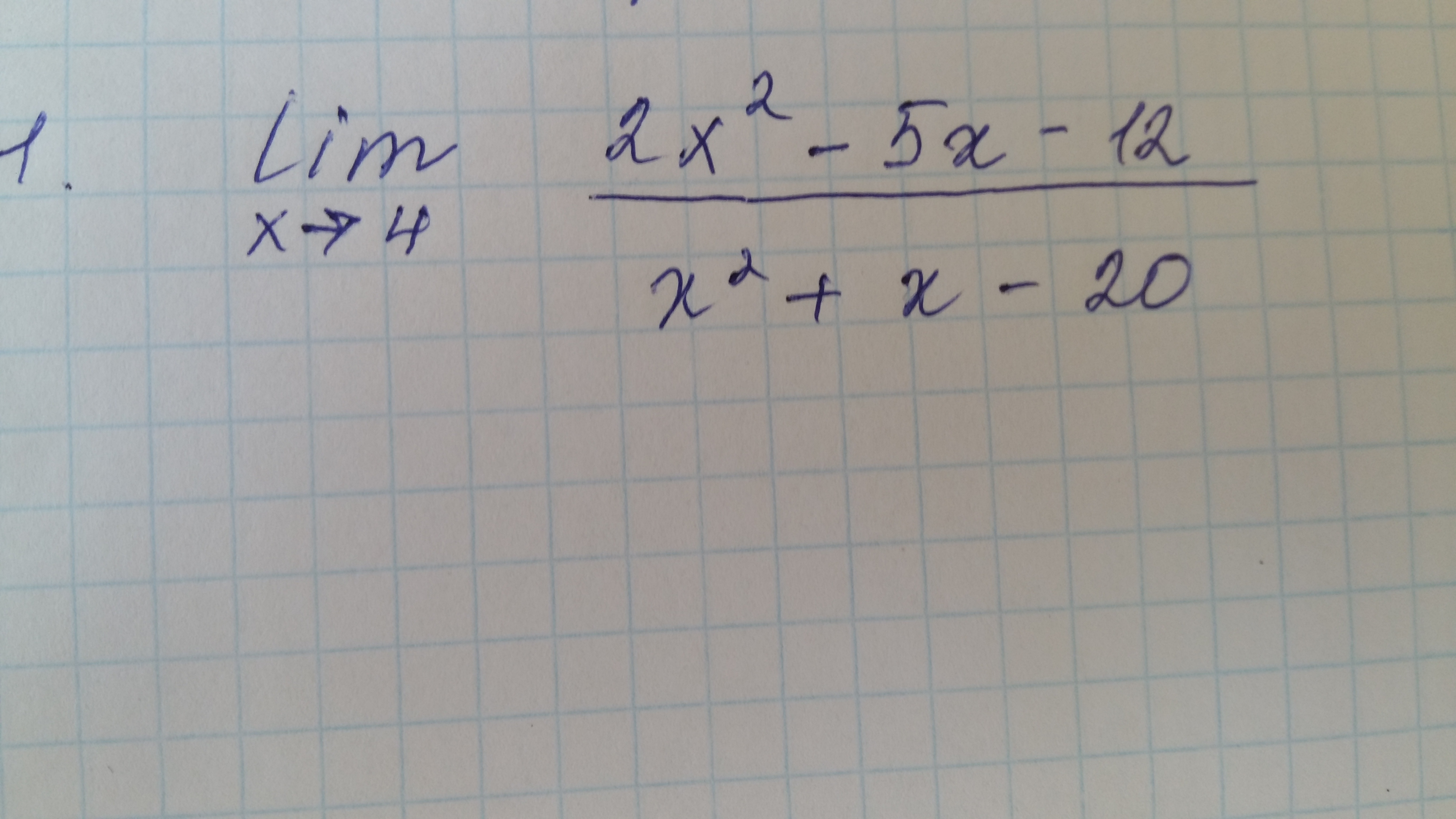

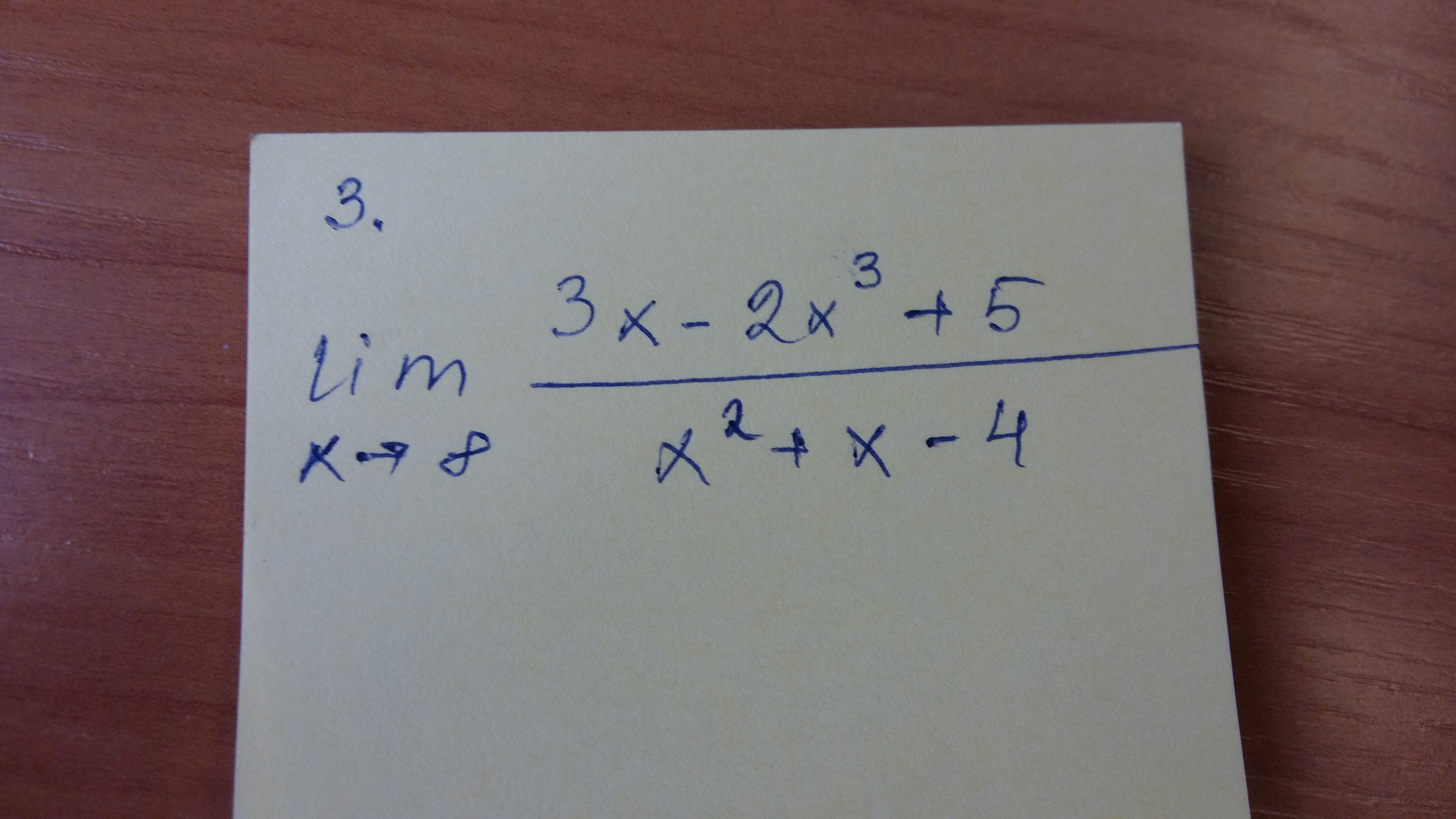
Ответы
Автор ответа:
0
1)

2)

3)

По правилу Лопиталя


2)
3)
По правилу Лопиталя
Похожие вопросы
Предмет: Русский язык,
автор: amalikova163
Предмет: Химия,
автор: boy2467
Предмет: Геометрия,
автор: pandoka042
Предмет: Физика,
автор: 1234567890200
Предмет: Алгебра,
автор: Kari1898