Question

Y=3x^+8x-3 8x-2y-6=0 вычислить площадь фигуры, ограниченной линиями.построить фигуру.

Answer 1

Площадь фигуры это определённый интеграл от разности функций ограничивающих эту фигуру. Находим пределы интегрирования или общие точки (лучше по графику, но можно и аналитически):
для этого из второго уравнения выразим у
8x-2y-6=0
-2y=-8x+6
y=(-8x+6)/-2=4x-3

3x²+8x-3=4x-3
3x²+8x-4x-3+3=0
3x²+4x=0
x(3x+4)=0
x=0   3x+4=0
         3x=-4
         x=-4/3
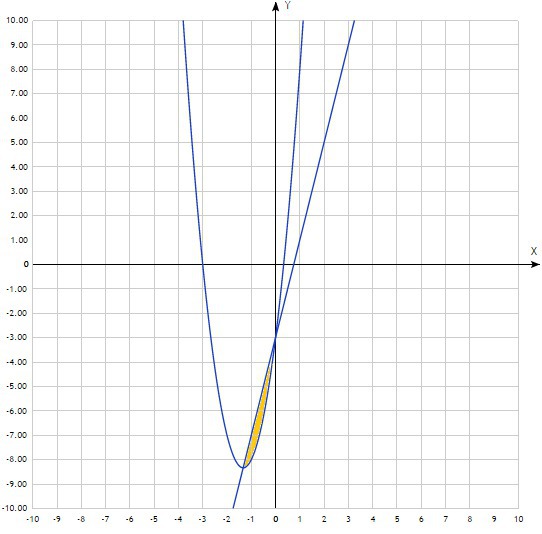
Теперь можем найти площадь фигуры. График лучше начертить, хотя бы для того чтобы представлять как выглядит фигура и какая из функций расположена выше. В нашем случае выше расположена функция y=4x-3, значит формула поиска площади выглядит так:
$S= intlimits^0_{- frac{4}{3} } {(4x-3-(3x^2+8x-3))} , dx = intlimits^0_{- frac{4}{3} }{(-3x^2-4x)} , dx =$
$=-x^3-2x^2|_{- frac{4}{3} }^0=0-(-(- frac{4}{3})^3-2*(- frac{4}{3} )^2)=- frac{64}{27} + frac{32}{9}= frac{-64+96}{27}=$
$= frac{32}{27}= 1 frac{5}{27}$

Ответ: 1 (5/27)