Предмет: Математика,
автор: SempreGioia
Подскажите, пожалуйста. Необходимо перейти к аналитическому виду заданной графиком функции. Заранее спасибо.
Приложения:
Ответы
Автор ответа:
0
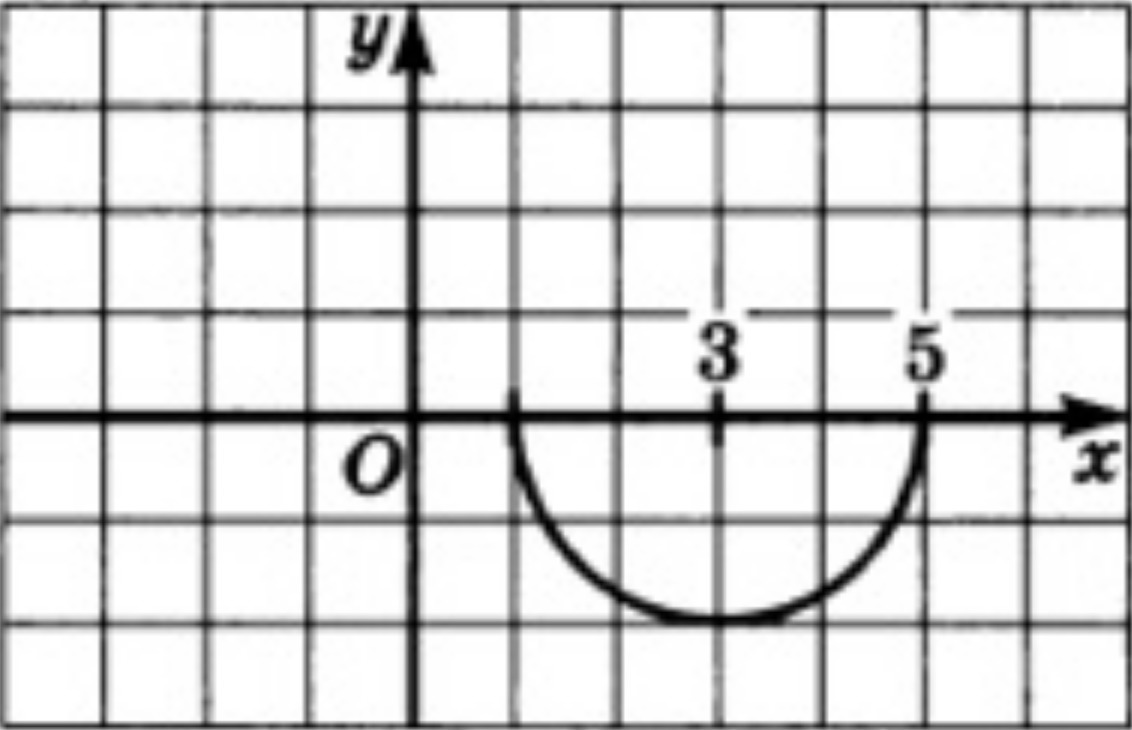
На графике изображена половина окружности, лежащая ниже оси ОХ.
Уравнение окружности
(x-x₀)²+(y-y₀)²=r²
(x₀;y₀) - координаты центра окружности, в нашем случае это (3;0)
r - радиус окружности, у нас это 2 (5-3=2).
Подставляем в уравнение
(x-3)²+(y-0)²=2²
(x-3)²+y²=4
y²=4-(x-3)²
y = √(4-(x-3)²) y = -√(4-(x-3)²)
Так как нас интересует половина окружности, расположенная ниже оси ОХ, то уравнение будет выглядеть так
y = - √(4-(x-3)²)
Уравнение окружности
(x-x₀)²+(y-y₀)²=r²
(x₀;y₀) - координаты центра окружности, в нашем случае это (3;0)
r - радиус окружности, у нас это 2 (5-3=2).
Подставляем в уравнение
(x-3)²+(y-0)²=2²
(x-3)²+y²=4
y²=4-(x-3)²
y = √(4-(x-3)²) y = -√(4-(x-3)²)
Так как нас интересует половина окружности, расположенная ниже оси ОХ, то уравнение будет выглядеть так
y = - √(4-(x-3)²)
Автор ответа:
0
Ничего, буду знать, как решать
Похожие вопросы
Предмет: Литература,
автор: snappi28384
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: tihonbro75
Предмет: Геометрия,
автор: 4РИМ
Предмет: Обществознание,
автор: ggfghfhhv