Question

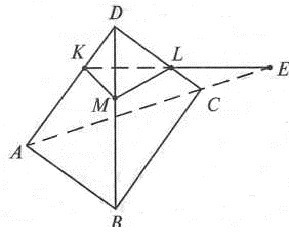
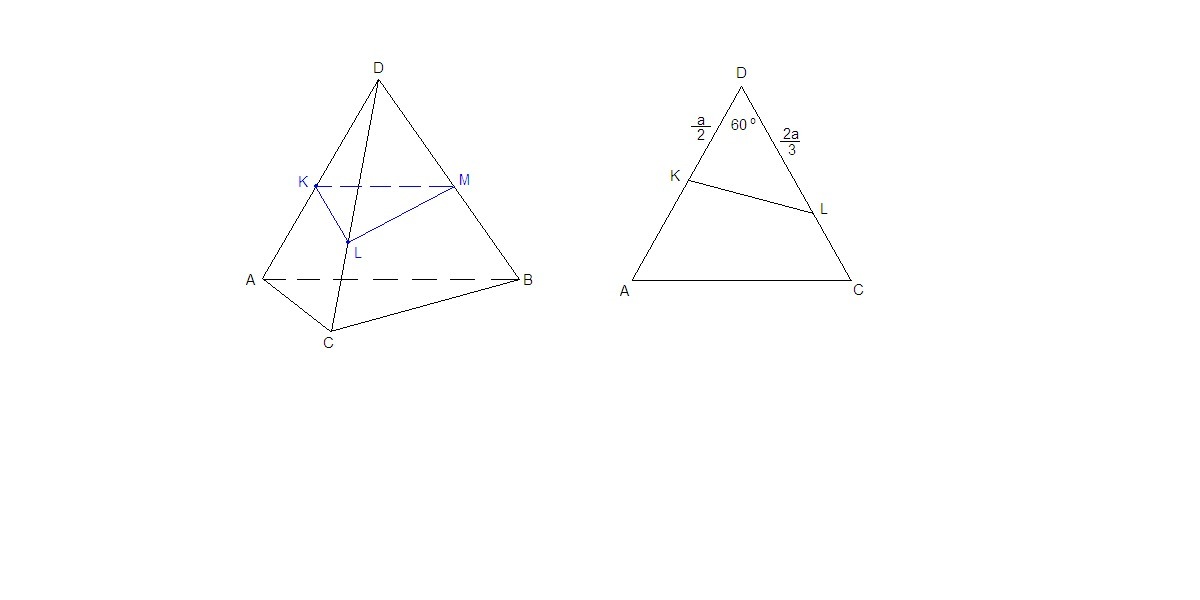
В тетраэдре DABC все ребра равны а, точка К ∈ АD и АК = КD, точка L ∈ DС и СL : LD =1:2 (рис. 1). Построено сечение КLМ, параллельное прямой АВ. Используя рисунок, ответьте на вопросы №№ 1 - 3.

1. Укажите линию пересечения плоскостей KLM и ACD.

2. Найдите
параллельные прямые.

3. Определите
периметр треугольника КLМ.

Answer 1

1. KLM ∩ ACD = KL

2. KM ║ AB

3. Так как К - середина AD и KM║ АВ, то КМ - средняя линия ΔADB, ⇒

КМ = АВ/2 = а/2.

CL : LD = 1 : 2, ⇒ DL = 2a/3.

KD = a/2

Из треугольника KLD по теореме косинусов:

KL² = DK² + DL² - 2DK·DL·cos 60°

KL² = a²/4 + 4a²/9 - 2 · a/2 · 2a/3 · 1/2 = a²/4 + 4a²/9 - a²/3 = a²/4 + a²/9

KL² = 13a²/36

KL = a√13/6

ML = KL = a√13/6

Pklm = ML + KL + KM = 2 · a√13/6 + a/2 = a(2√13 + 3)/6