Предмет: Геометрия,
автор: KovAlfie
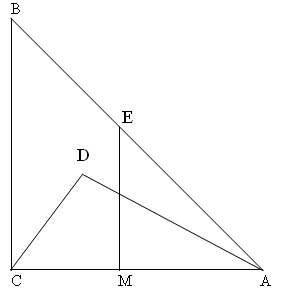
На гипотенузе АВ прямоугольного треугольника АВС взята точка Е, а внутри треугольника АВС взята точка D. ЕМ перпендикулярно АС, АМ=СМ, угол В равен 45 градусам, угол СDА равен 90 градусам, угол DСА равен 60 градусам. Доказать: ЕМ=DC.
Приложения:
Ответы
Автор ответа:
92
В прямоугольном треугольнике сумма острых углов равна 90. Если угол В равен 45, то угол А тоже 45. В треугольнике ЕАМ угол м - прямой, угол А = 45, значит и угол Е=45. Треугольник ЕАМ - равнобедренный, а в равнобедренном треугольнике боковые стороны равны. Значит ЕМ=АМ.
А в треугольнике АДС угол Д- прямой, угол С=60, значит угол САД равен 30. А в прямоугольном треугольнике катет, лежащий против угла в 30 градусов равен половине гипотенузы. Значит, СД=1/2 АС. Но АМ=СМ =ЕМ = 1/2АС.
Отсюда, СД=ЕМ
Похожие вопросы
Предмет: Русский язык,
автор: MoChalka2018
Предмет: Русский язык,
автор: няшка8909
Предмет: Русский язык,
автор: ильякозгов
Предмет: Русский язык,
автор: svechkanat
Предмет: Математика,
автор: coldplayer1725