Предмет: Алгебра,
автор: Аноним
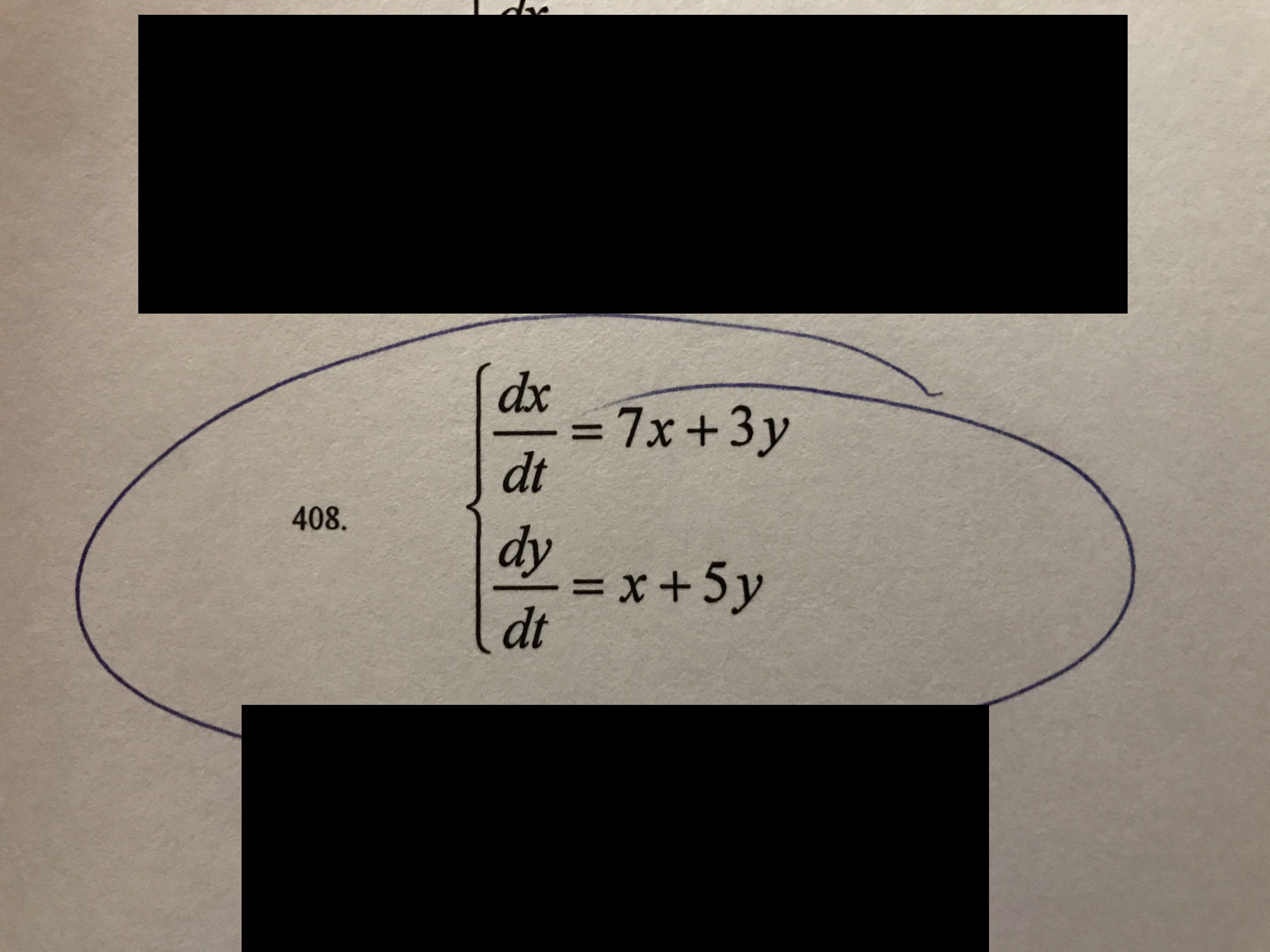
Помогите найти общее решение системы дифференциальных уравнений
Приложения:
Ответы
Автор ответа:
0
составим матрицу:
характеристическая матрица:
характеристическое уравнение:
найдем собственный вектор для собственного числа
вторая строка есть следствие первой, по этому:
положим
таким образом
найдем собственный вектор для собственного числа
вторая строка есть следствие первой, по этому:
положим
таким образом
два частных решения
или:
Похожие вопросы
Предмет: Українська мова,
автор: wonivika
Предмет: Математика,
автор: zakhat73
Предмет: Право,
автор: viktoria6020
Предмет: Обществознание,
автор: madik1979
Предмет: Алгебра,
автор: ksal28