Периметр параллелограмма равен 30 см. Биссектрисы углов В и С пересекают сторону АД в одной точке. Найти длину короткой стороны параллелограмма, выразив ответ в сантиметрах.
Ответы
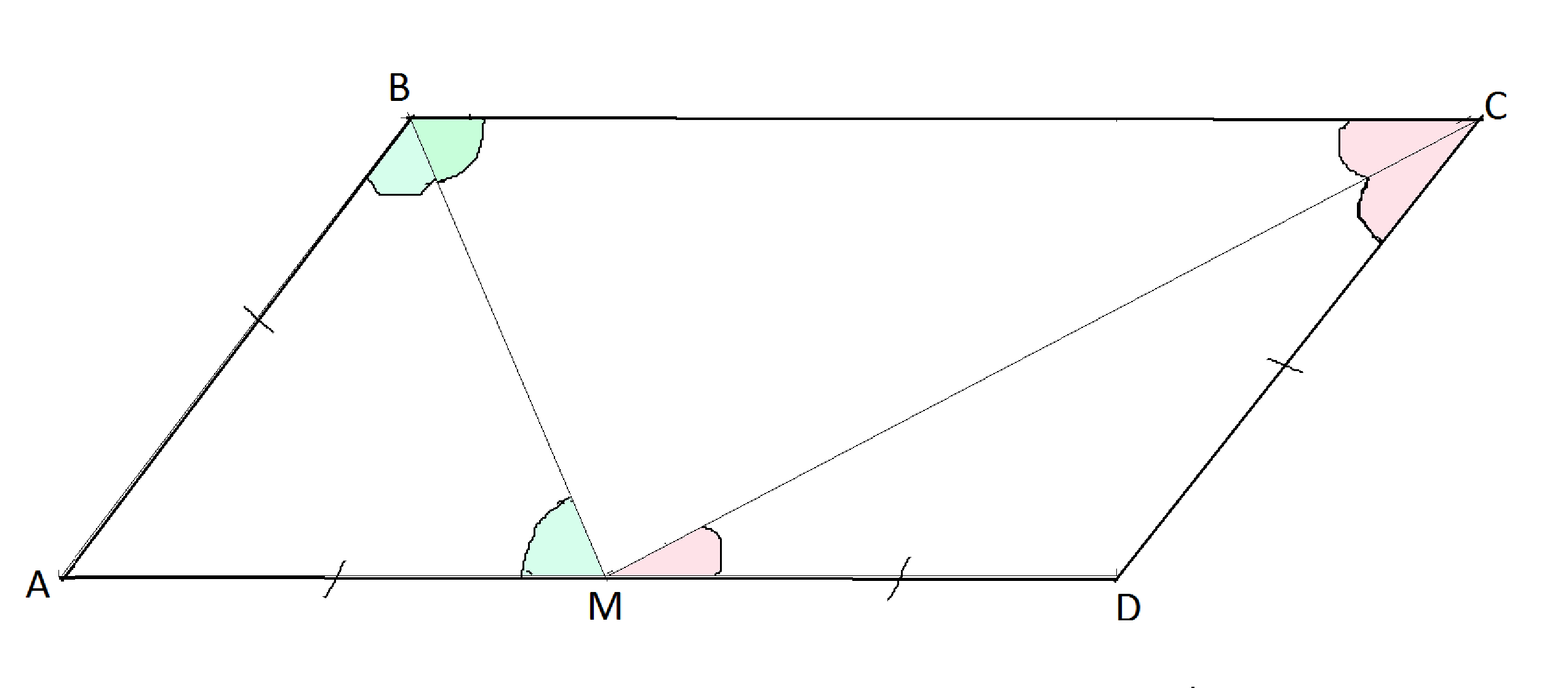
Сделаем рисунок к задаче.
Обозначим вершины параллеограмма привычными буквами АВСD.
Проведем биссектрисы углов В и С, которые пересекутся на АD в точке М.
Биссектрисы образовали со сторонами параллелограмма треугольники, причем
∠ СВМ= ∠ АМВ по свойству углов при пересечении параллельных прямых и секущей, а
∠ АВМ= ∠МВС - как половины угла В.
То же самое с углами ВСМ и СМD.
Раз углы при основании ВМ Δ АВМ и основании СМ Δ СМD равны,
оба этих треугольника - равнобедренные.
В треугольнике АВМ сторона АВ равна стороне АМ,
В треугольнике МDС сторона МD равна стороне СD.
Но АВСD- параллелограмм, и стороны АВ и CD равны по определению.
Следовательно, АМ=MD и АD=2АВ ( или 2 CD, что одно и то же)
Р АВСD= 2( АВ+АD) Подставим в значение периметра 2 АВ вместо AD.
Р АВСD= 2( АВ+2АВ)
30= 6 АВ
АВ=5 см
Ответ: Длина короткой стороны параллелограмма равна 5 см