помогите с геометрией хоть что нить решите напишите мне с решением пожалуйста
Ответы
Задание решено Пользователем Nina200 Светило науки
Исправлено оформление и опечатка.
1) Скалярное произведение векторов равно произведению длин векторов на косинус угла между ними.
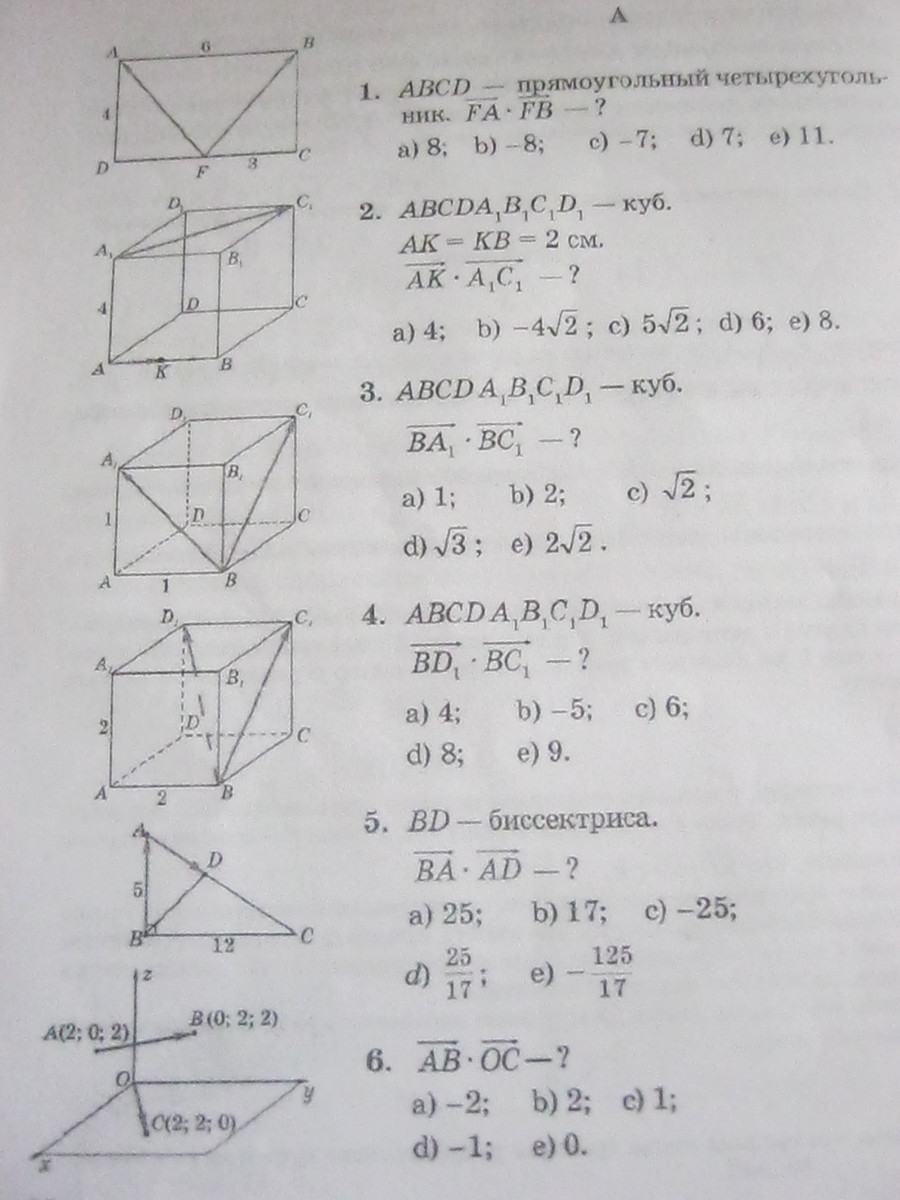
↑FA · ↑FB = |↑FA| · |↑FB| · cos∠AFB,
из прямоугольного треугольника ADF по теореме Пифагора
AF =√(3² + 4²) = 5, FB = FA = 5 (ΔADF = ΔACF по двум катетам),
из треугольника AFB по теореме косинусов:
cos∠AFB = (FA² + FB² - AB²) / (2FA·FB) =
= (5² + 5² - 6²) / (2 · 5 · 5) = 7/25
↑FA · ↑FB = 5 · 5 · 7/25 = 7
Ответ: d)
2) ↑АК · ↑А₁С₁ = ↑АК ·↑АС = |↑АК| · |↑АС| · cos∠CAB
АС - диагональ квадрата, диагональ квадрата больше стороны в √2 раз, поэтому АС = 4√2. Угол между диагональю и стороной 45°.
↑АК · ↑АС = 2 · 4√2 · √2/2 = 8
Ответ: е)
3) ВА₁ и ВС₁ диагонали квадратов, поэтому больше сторон в √2 раз,
ВА₁ = ВС₁ = √2
треугольник А₁ВС₁ равносторонний, все углы по 60°, cos∠A₁BC₁ = 1/2,
↑ВА₁ · ↑ВС₁ = |↑BA₁| · |↑BC₁| · cos∠A₁BC₁ = √2 · √2 · 1/2 = 1
Ответ: а)
4) ВD₁ - диагональ куба, она равна корню квадратному из суммы квадратов трёх его измерений:
ВD₁ = √(2² + 2² + 2²) = √12 = 2√3
ВС₁ - диагональ квадрата, ВС₁ = 2√2
ΔВD₁С₁: ∠BC₁D₁ = 90°,
cos∠C₁BD₁ = BC₁ / BD₁ = 2√2 / (2√3)= √2/√3
↑ВD₁ · ↑ВС₁ = |BD₁| · |BC₁| · cos∠C₁BD₁ = 2√3 · 2√2 · √2/√3 = 8
Ответ: d)
5) По теореме Пифагора АС = √(АВ² + ВС²) = √(5² + 12²) = 13,
угол между векторами тупой, cosα = - 5/13,
биссектриса ВD разделила гипотенузу на 2 отрезка АD и DС, пусть АD = х, тогда DС = 13-х. По свойству биссектрисы х/5 = (13-х)/12
5 · (13 - х) = 12х
17х = 65
х = 65/17
↑ВА · ↑АD = |↑BA| · |↑AD| · cosα = 5 · 65/17 · ( - 5/13) = - 125/17
Ответ: е)
6) Вектор АВ имеет координаты (-2; 2; 0),
вектор ОС имеет координаты (2; 2; 0)
↑АВ · ↑ОС = -2 · 2 + 2 · 2 + 0 · 0 = - 4 + 4 + 0 = 0
Ответ: е)
Подробнее - на Znanija.com - https://znanija.com/task/2054040#readmore