Предмет: Геометрия,
автор: 01albina01
СРОЧНО!!!! ПОМОГИТЕ!!!! ПОЖАЛУЙСТА!!!! С РИСУНКАМИ КО ВСЕМ ЗАДАЧАМ!!!!
1. В равнобедренной трапеции диагонали взаимно перпендикулярны. Высота трапеции равна 8 см. Нвйти периметр трапеции, если боковая сторона равна 12 см.
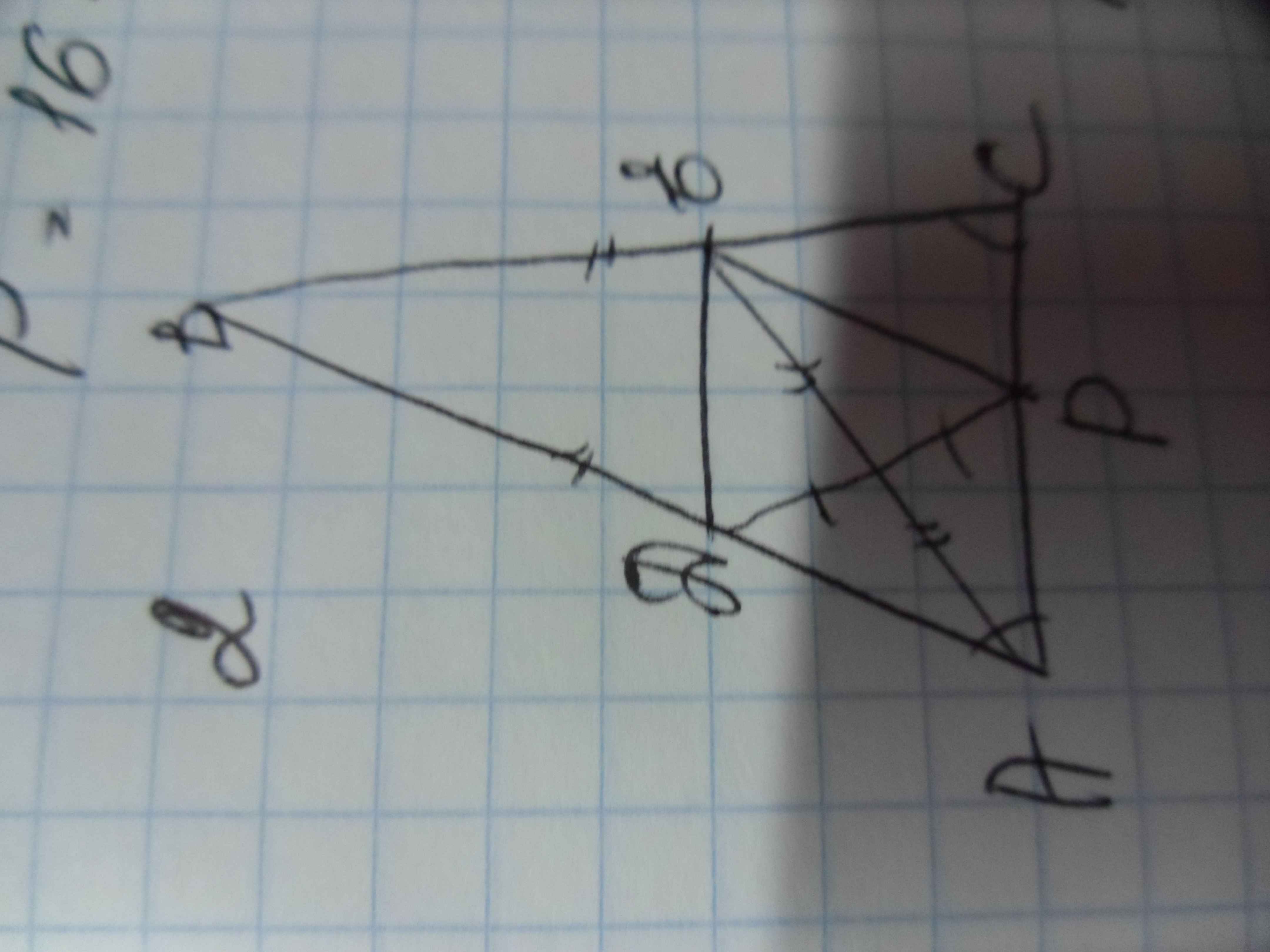
2. Дан равнобедренный треугольник АВС с основанием АС. На сторонах АВ, ВС, АС отмечены точки D, E, P соответственно так, что отрезки АЕ и DР имеют общую середину. Доказать, что угол DEP = углу BCA.
Ответы
Автор ответа:
0
1. Если диагонали трапеции взаимно перпендикулярны ,то высота трапеции равна полусумме ее оснований .т.к высота равна 8 см ,то сумма оснований равна 8*2=16 см
Р=16+12*2=40 см
2.Рассмотрим четырехугольник АDEP-т.к его диагонали точкой пересечения делятся делятся пополам это параллелограмм.
⇒ противолежащие углы равны т.е ∠DAP=∠DEP
а т.к треугольник АВС равнобедренный .то углы при основании у него равны ∠ВАС=∠ВСА .отсюда ∠А=∠Е=∠С т.е ∠DEP=∠ВCA , что и требовалось доказать
Р=16+12*2=40 см
2.Рассмотрим четырехугольник АDEP-т.к его диагонали точкой пересечения делятся делятся пополам это параллелограмм.
⇒ противолежащие углы равны т.е ∠DAP=∠DEP
а т.к треугольник АВС равнобедренный .то углы при основании у него равны ∠ВАС=∠ВСА .отсюда ∠А=∠Е=∠С т.е ∠DEP=∠ВCA , что и требовалось доказать
Приложения:
Похожие вопросы
Предмет: Биология,
автор: ksyha1578
Предмет: Литература,
автор: kakashka12534
Предмет: Химия,
автор: dianaalacev
Предмет: Математика,
автор: Anastasuya
Предмет: Алгебра,
автор: marina975