Question

Расставьте все числа от 2 до 6 в
больших кругах на стрелках так, чтобы сумма чисел на стрелках, входящих в любой маленький кружок, равнялась сумме чисел на стрелках, выходящих из того же кружка

Answer 1

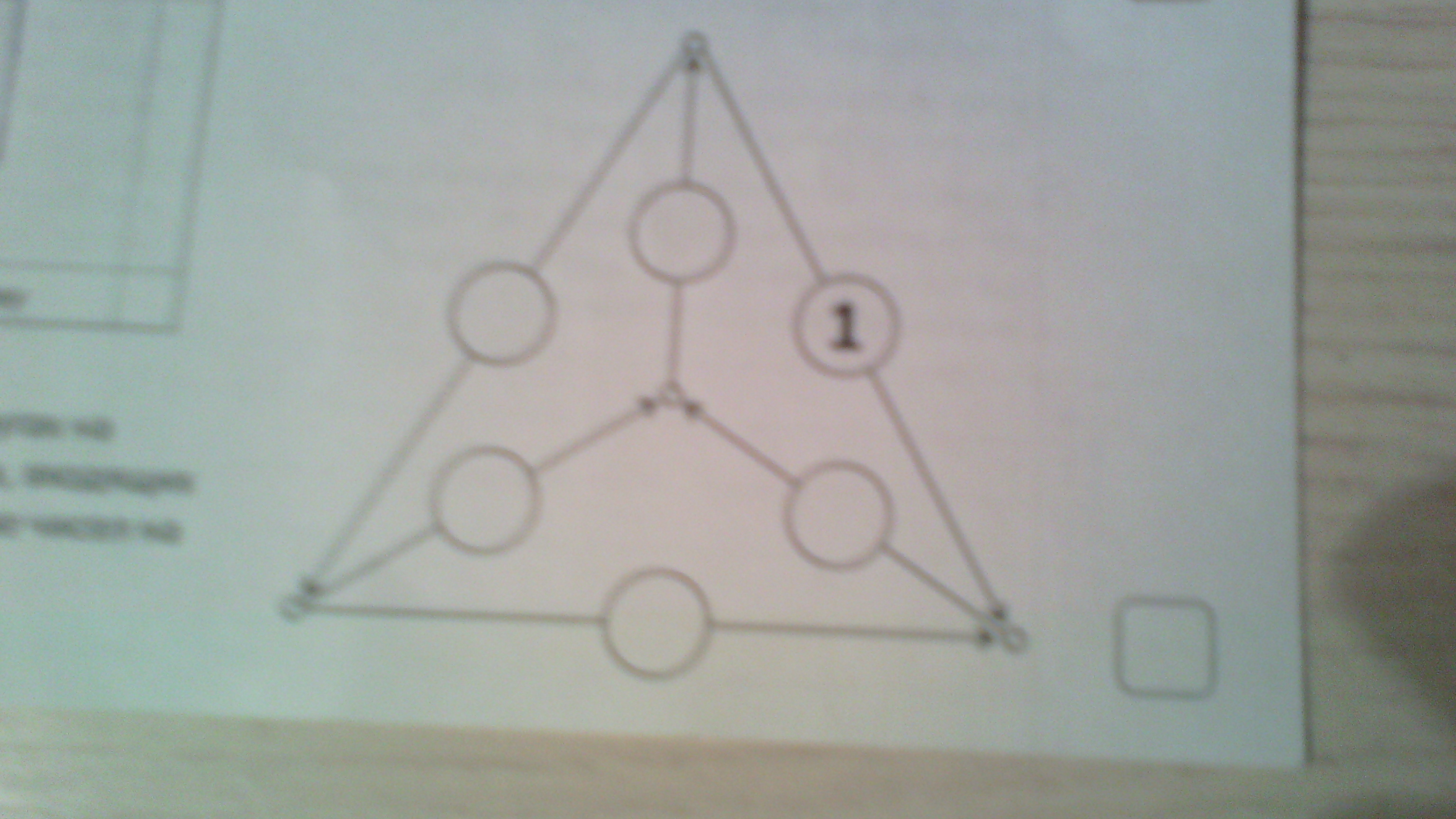
Легко видеть, что правая нижняя цифра равна сумме правой верхней и нижней цифр, а верхняя цифра, в свою очередь, равна правой нижней плюс левая нижняя, значит, скорее всего,  верхняя цифра является максимальной, т.е. 6. Тогда левая верхняя 5, и т.д. Получаем следующую расстановку
  6
5  1
2  4
  3
Лего убедиться, что эта схема годится:
Для верхнего маленького кружка: 6=5+1
Для среднего маленького кружка: 2+4=6
Для левого нижнего маленького кружка: 5=2+3
Для правого нижнего маленького кружка: 3+1=4.