Нужно решить два уравнения. Один с логарифмами. У меня не получается, не могу понять где ошибся...
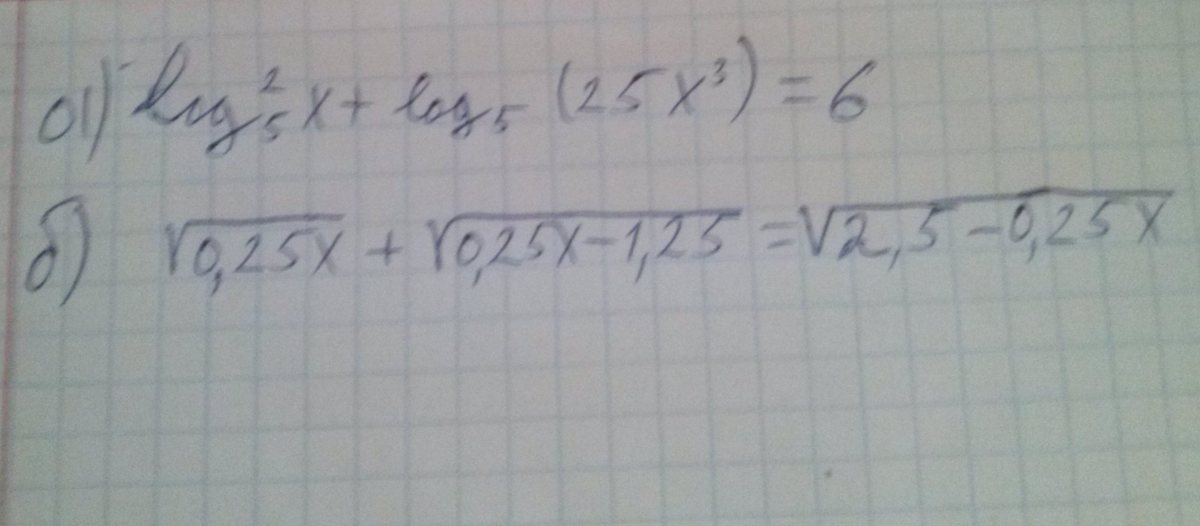
Ответы
log5^2x +log5 25+log5x^3=6
log5^2x+2+3log5x-6=0
log5^2x +3log5x-4=0
log5x=t
t^2+3t-4=0
t1=4, t2=-1
log5x=4
x=5^4=625
log5x=-1
x=1/5
а) (log5 (x) )^2 + log5 (25) + log5 (x^3) = 6
вводим новую переменную а = log5(x)
a^2 + 2 + 3a - 6 = 0
a^2 + 3a - 4 = 0
по т.Виета a1 = -4 a2 = 1
log5(x) = 1 log5(x) = -4
x1 = 5 x2 = 5^(-4) = 1/625 = 0.0016
b)-----------------------------------------------------
возведем обе части равенства в квадрат, слева получим формулу --- квадрат суммы...
0.25x + 2корень(0.25x*(0.25x-1.25)) + 0.25x - 1.25 = 2.5 - 0.25x
2корень(0.25x*(0.25x-1.25)) = - 0.5x + 1.25 + 2.5 - 0.25x
2корень(0.25x*(0.25x-1.25)) = - 0.75x + 3.75 и еще раз возведем в квадрат...
4*0.25x*(0.25x-1.25) = 0.75*0.75*x^2 - 2*0.75*3.75*x + 3.75*3.75
чтобы избавиться от дробей ---умножим обе части равенства на 16...
16x*0.25x - 16x*1.25 = 9x^2 - 90x + 225
4x^2 - 20x = 9x^2 - 90x + 225
9x^2 - 4x^2 + 20x - 90x + 225 = 0
5x^2 - 70x + 225 = 0
x^2 - 14x + 45 = 0
по т.Виета x1 = 9 x2 = 5