Предмет: Математика,
автор: DashaBokhonko
исследовать ряд на абсолютную и условную сходимость
Приложения:
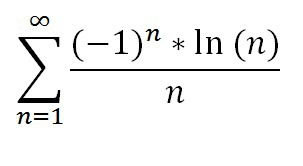
Ответы
Автор ответа:
0
Так как ряд из абсолютных величин (модулей) расходится, то нет абсолютной сходимости. Но выполняются условия признака Лейбница. Поэтому заданный знакочередующийся ряд сходится условно.
Похожие вопросы
Предмет: Русский язык,
автор: finoloboni
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: trohimecmaksim524
Предмет: Геометрия,
автор: Veronika789
Предмет: Математика,
автор: Yeseniya545