Предмет: Алгебра,
автор: AhnSoHee
Помогите решить алгебру
Приложения:
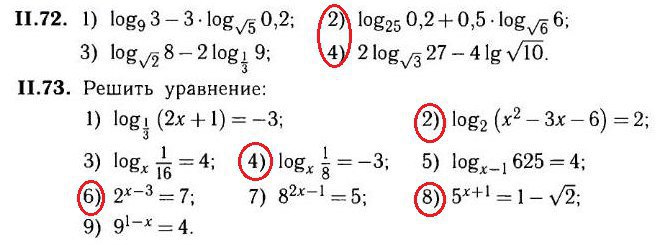
Ответы
Автор ответа:
0
11.72.
2) log25_0,2 + 0,5 log√6_6 = log5^2_1/5 + 0,5 log6^1/2_6 =
= - 1/2 + 0,5 * 2 = - 0,5 + 1= 0,5.
4) 2 log√3_27 - 4 lg√10 = 2 log3^1/2_ 3^2 - 4 lg10^1/2 = 2*2*2 - 4*1/2 =6.
11.73.
2) log2_(x^2 - 3x - 6) = 2;
log2_(x^2 - 3x - 6) = log2_4;
x^2 - 3x - 6 = 4;
x^2 - 3x - 10 = 0;
x1= 5;
x2 = 2.
Проверка корней.
x = 5.
x^2 - 3x - 6 > 0;
25 - 15 - 6 = 4 > 0;
x= - 2;
x^2 - 3x - 6 = 4 + 6 - 6 = 4 > 0.
x = -2; x = 5.
4) logx_1/8 = - 3;
x^(-3) = 1/8;
x^(-3) = 2^(-3);
x = 2.
6( 2^(x-3) = 7;
2^(x-3) = 2^log2_7;
x - 3 = log2_7.
8)5^(x+1) = 1 - √2;
5^(x+1) = 5^log5_( 1 - √2);
x + 1 = log5_( 1 - √2);
x = log5_( 1 - √2) - 1= log5_((1 - √2) / 5)
2) log25_0,2 + 0,5 log√6_6 = log5^2_1/5 + 0,5 log6^1/2_6 =
= - 1/2 + 0,5 * 2 = - 0,5 + 1= 0,5.
4) 2 log√3_27 - 4 lg√10 = 2 log3^1/2_ 3^2 - 4 lg10^1/2 = 2*2*2 - 4*1/2 =6.
11.73.
2) log2_(x^2 - 3x - 6) = 2;
log2_(x^2 - 3x - 6) = log2_4;
x^2 - 3x - 6 = 4;
x^2 - 3x - 10 = 0;
x1= 5;
x2 = 2.
Проверка корней.
x = 5.
x^2 - 3x - 6 > 0;
25 - 15 - 6 = 4 > 0;
x= - 2;
x^2 - 3x - 6 = 4 + 6 - 6 = 4 > 0.
x = -2; x = 5.
4) logx_1/8 = - 3;
x^(-3) = 1/8;
x^(-3) = 2^(-3);
x = 2.
6( 2^(x-3) = 7;
2^(x-3) = 2^log2_7;
x - 3 = log2_7.
8)5^(x+1) = 1 - √2;
5^(x+1) = 5^log5_( 1 - √2);
x + 1 = log5_( 1 - √2);
x = log5_( 1 - √2) - 1= log5_((1 - √2) / 5)
Похожие вопросы
Предмет: Математика,
автор: hikituy123
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: adinarahat
Предмет: География,
автор: деврчкасдомашкой
Предмет: Алгебра,
автор: alenkailienko