Предмет: Геометрия,
автор: igor03123
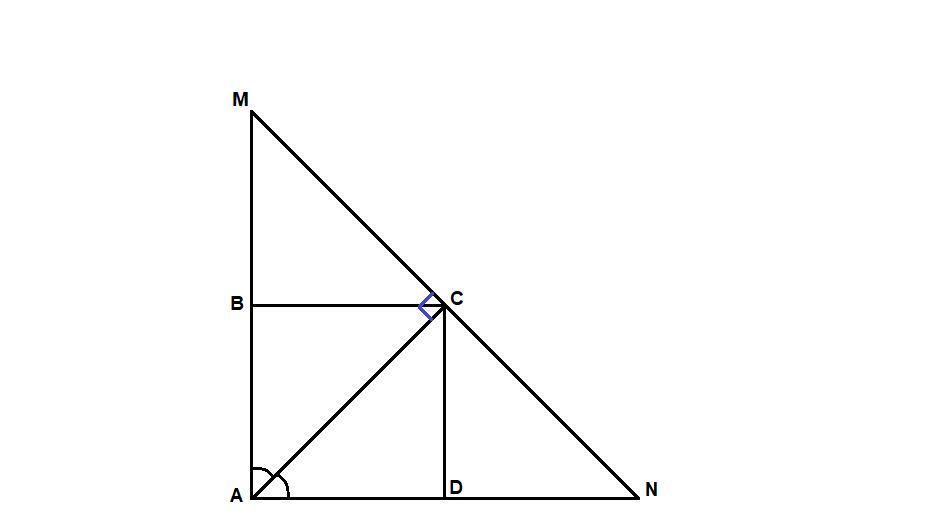
Через конечную точку C диагонали AC=24,2 ед. изм. квадрата ABCD проведена прямая перпендикулярно диагонали AC. Проведённая прямая пересекает прямые AB и AD в точках M и N соответственно.
Определи длину отрезка MN.
Ответы
Автор ответа:
0
Ответ:
48,4 ед. изм.
Объяснение:
Рассмотрим треугольник MAN:
∠MAN = 90°
АС - биссектриса треугольника, так как диагонали квадрата лежат на биссектрисах его углов,
АС - высота треугольника, так как MN⊥АС по условию, значит
треугольник MAN равнобедренный и АС является так же его медианой.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, т.е.
MN = 2AC = 2 · 24,2 = 48,4 ед. изм.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: woowosopsososo
Предмет: Математика,
автор: dyhffgvc1
Предмет: Астрономия,
автор: pashenkotatyana01
Предмет: Геометрия,
автор: 4РИМ
Предмет: Алгебра,
автор: svintsova01