Question

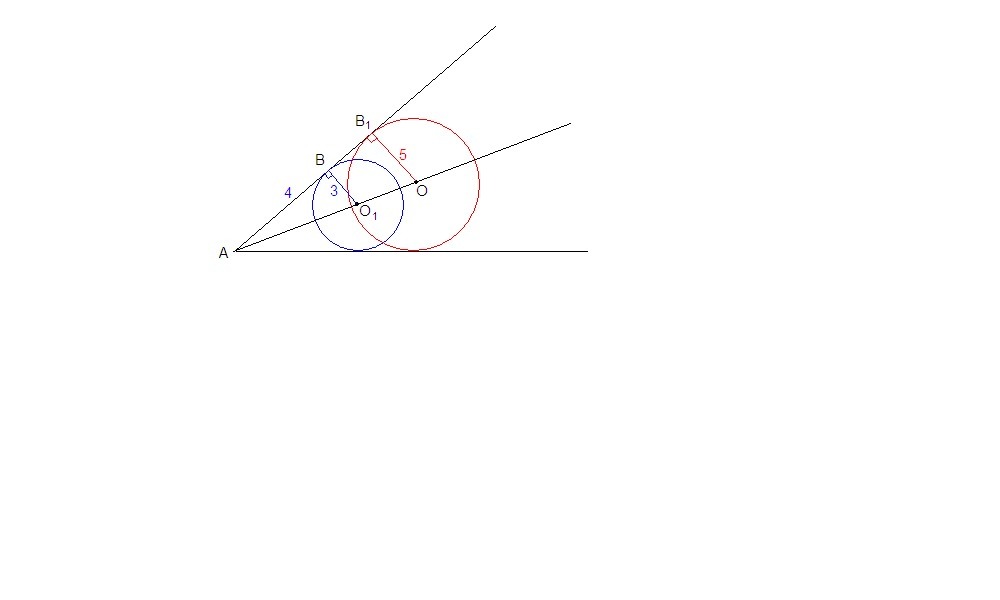
две окружности с центрами в точках о и о1 и радиусами 5 и 3 соответственно касаются сторон угла А(В и В1- точки касания). Найдите расстояние между центрами окружностей, если АВ1 = 4.

Answer 1

Радиус, проведенный в точку касания, перпендикулярен касательной, ⇒
∠О₁В₁А = ∠ОВА = 90°.
ΔО₁В₁А - прямоугольный, египетский, значит АО₁ = 5.
∠А - общий для треугольников АО₁В₁ и АОВ, значит они подобны по двум углам.
О₁В₁ : ОВ = АО₁ : АО
3 : 5 = 5 : АО
АО = 5 · 5 / 3 = 25/3
ОО₁ = АО - АО₁ = 25/3 - 5 = 10/3
Так как расстояние между центрами меньше суммы радиусов, то окружности пересекаются.