Предмет: Алгебра,
автор: timon7890
избавьтесь от иррациональности в дроби
Приложения:
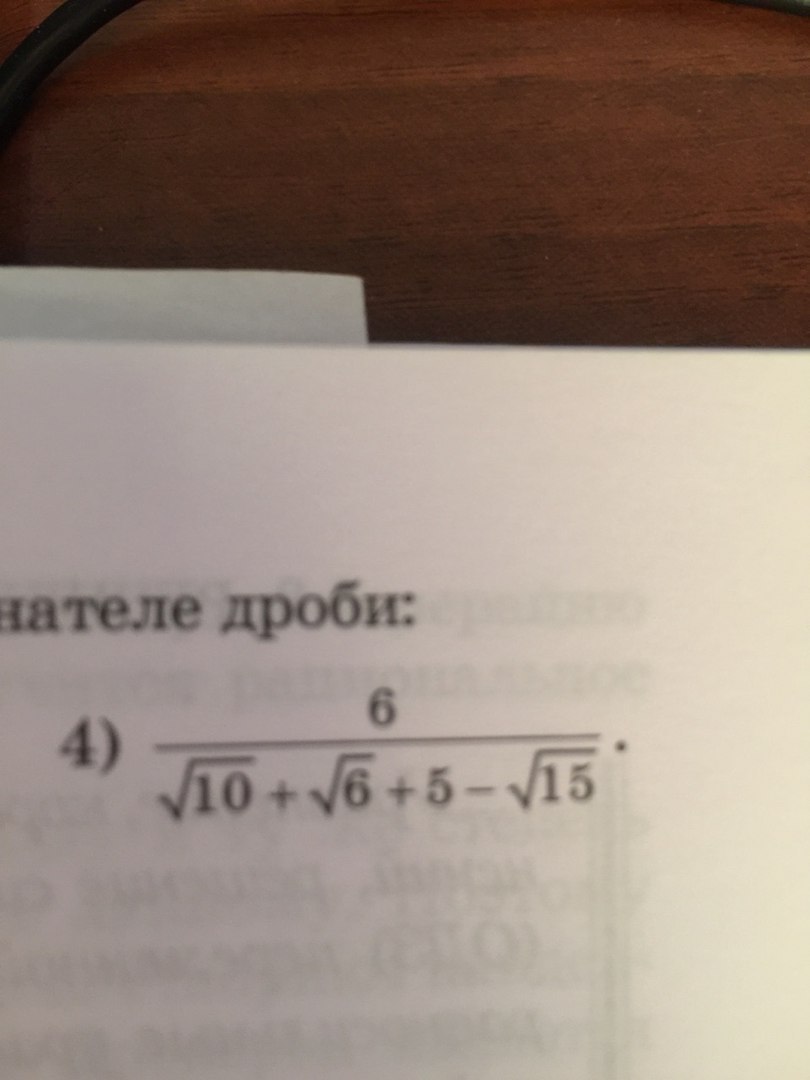
Ответы
Автор ответа:
0
Чтобы в знаменателе исчезли корни, надо и числитель , и знаменатель умножить на такое выражение, чтобы в знаменателе получилась разность квадратов. Для нашего случая надо это действо выполнить не один раз. Для начала возимся со знаменателем.
√10 + √6 + 5 - √15 = ( √10 + 5) + ( √6 - √15) =
= (√10 + √25)+ ( √6 - √15) = √5(√2 + √5) + √3(√2 - √5)
Теперь и числитель, и знаменатель умножим на
√5(√2 + √5) - √3(√2 - √5)
Знаменатель = ( √5(√2 + √5) + √3(√2 - √5) )( √5(√2 + √5) - √3(√2 - √5))
= (√5(√2 + √5) )² - (√3(√2 - √5))² = 5(2 + 2√10 + 5) -3(2 - 2√10 +5) =
=35 +10√10 - 21 + 6√10 = 14 +16√10= 2(7 + 8√10)
Теперь снова умножаем и числитель, и знаменатель на (7 - 8√10)
Получим знаменатель = 2(49 -640) = -1182. Ну, а числитель будет
=6(√5(√2 + √5) - √3(√2 - √5)) (7 - 8√10)
Дробь на 6 можно сократить.
Ответ: (√5(√2 + √5) - √3(√2 - √5)) (7 - 8√10)/197
√10 + √6 + 5 - √15 = ( √10 + 5) + ( √6 - √15) =
= (√10 + √25)+ ( √6 - √15) = √5(√2 + √5) + √3(√2 - √5)
Теперь и числитель, и знаменатель умножим на
√5(√2 + √5) - √3(√2 - √5)
Знаменатель = ( √5(√2 + √5) + √3(√2 - √5) )( √5(√2 + √5) - √3(√2 - √5))
= (√5(√2 + √5) )² - (√3(√2 - √5))² = 5(2 + 2√10 + 5) -3(2 - 2√10 +5) =
=35 +10√10 - 21 + 6√10 = 14 +16√10= 2(7 + 8√10)
Теперь снова умножаем и числитель, и знаменатель на (7 - 8√10)
Получим знаменатель = 2(49 -640) = -1182. Ну, а числитель будет
=6(√5(√2 + √5) - √3(√2 - √5)) (7 - 8√10)
Дробь на 6 можно сократить.
Ответ: (√5(√2 + √5) - √3(√2 - √5)) (7 - 8√10)/197
Автор ответа:
0
минус будет перед выражением тогда?
Похожие вопросы
Предмет: Математика,
автор: annyshkanna4
Предмет: Алгебра,
автор: ashibomashido
Предмет: Қазақ тiлi,
автор: anastasia436369
Предмет: Математика,
автор: Dinalev
Предмет: Биология,
автор: uahxhx