Предмет: Алгебра,
автор: zzzfd
Точка M, двигаясь против часовой стрелки по окружности x2 + y2 = 16, сорвалась с неё и при дальнейшем свободном движении пересекла ось ординат в точке (0; 8). Определите ординату точки окружности, с которой сорвалась точка M.
Ответы
Автор ответа:
0
Точка полетит по касательной к траектории в точке отрыва.
Тогда ΔОАВ -- прямоугольный.
Составим систему из двух уравнений:

Ответ: y = 2.
Тогда ΔОАВ -- прямоугольный.
Составим систему из двух уравнений:
Ответ: y = 2.
Приложения:
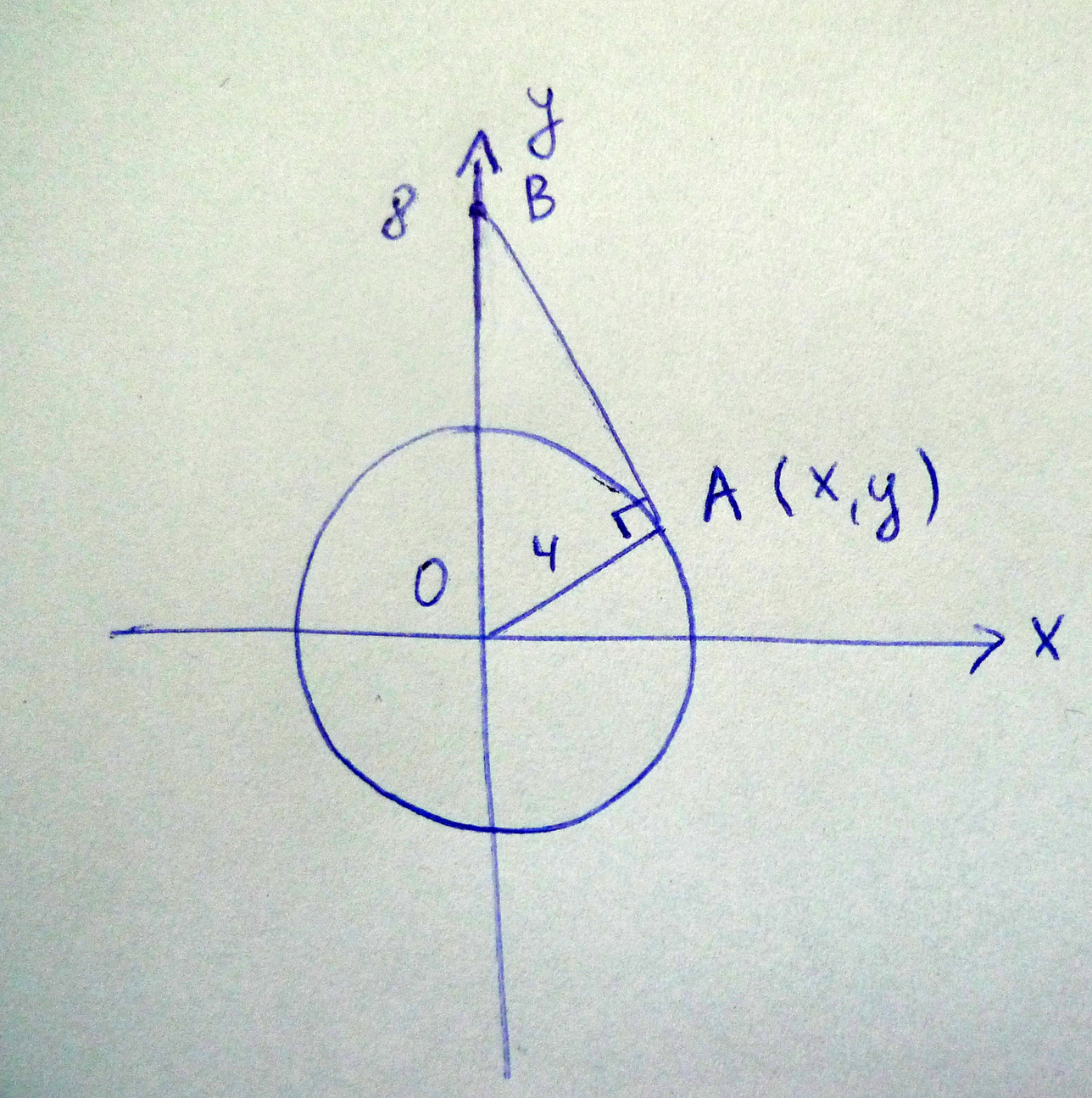
Похожие вопросы
Предмет: Физика,
автор: BettyDream
Предмет: Математика,
автор: yarikchernov00
Предмет: Геометрия,
автор: misterkokos5
Предмет: Математика,
автор: nicole87