Предмет: Геометрия,
автор: school123452
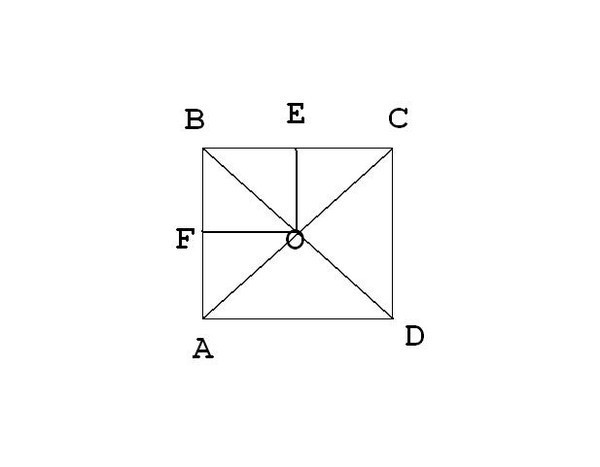
Через точку пересечения диагоналей квадрата проведены 2 взаимно перпендикулярные прямые. Доказать, что точки пересечения этих прямых со сторонами квадрата, являются вершинами еще одного квадрата.Через точку пересечения диагоналей квадрата проведены 2 взаимно перпендикулярные прямые.
Приложения:
Ответы
Автор ответа:
0
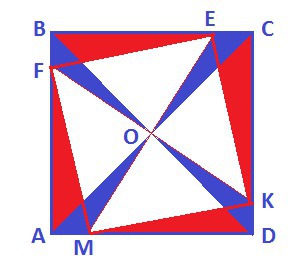
Диагонали АС и BD - равны и перпендикулярны.
Продолжаем прямые OF и OE до пересечения с противоположными сторонами и получаем перпендикулярные прямые FK и ME.
Получаем секущую прямую между двумя параллельными сторонами.
Четыре треугольника - равны - AFM, BEF, CKE, DMK.
Значит равны и их гипотенузы - стороны четырехугольника FEKM.
Получили фигуру - стороны равны, диагонали и равны и перпендикулярны - фигура = квадрат.
Продолжаем прямые OF и OE до пересечения с противоположными сторонами и получаем перпендикулярные прямые FK и ME.
Получаем секущую прямую между двумя параллельными сторонами.
Четыре треугольника - равны - AFM, BEF, CKE, DMK.
Значит равны и их гипотенузы - стороны четырехугольника FEKM.
Получили фигуру - стороны равны, диагонали и равны и перпендикулярны - фигура = квадрат.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: kovalcdiana
Предмет: Биология,
автор: igorsulak35
Предмет: Математика,
автор: csgotup
Предмет: Математика,
автор: almirabaibulato
Предмет: Математика,
автор: djdnsjdjdj