Question

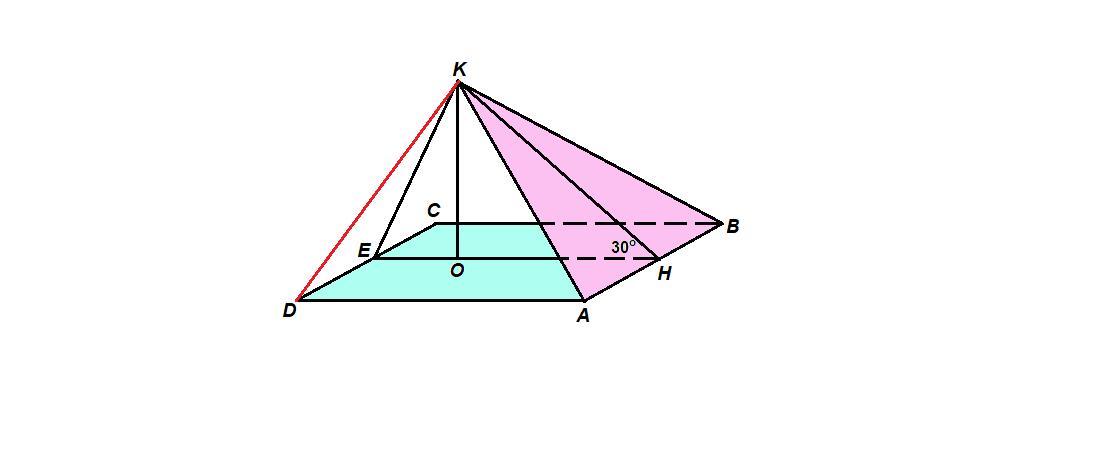
Угол между плоскостями равностороннего треугольника abk и квадрата abcd 30 градусов. Найдите рассояние kd, если ab=6 м

Answer 1

Ответ:    3√2 м

Объяснение:

Пусть Н - середина АВ, Е - середина CD.

Тогда КН - медиана и высота равностороннего треугольника АКВ,

КН⊥АВ.

ЕН - отрезок, соединяющий середины противоположных сторон квадрата, поэтому ЕН = ВС = 6 м  и ЕН║ВС, значит

ЕН⊥АВ, ⇒

∠КНЕ = 30° - линейный угол двугранного угла между плоскостями треугольника и квадрата.

КН = АВ√3/2 = 6√3/2 = 3√3 м как высота равностороннего треугольника АКВ,

Из ΔКНЕ по теореме косинусов:

KE² = KH² + EH² - 2·KH·EH·cos30°

KE² = (3√3)² + 6² - 2 · 3√3 · 6 · √3/2 = 27 + 36 - 54 = 63 - 54 = 9

KE = 3 м

ОЕ⊥CD, ОЕ - проекция КЕ на плоскость (АВС), ⇒

КЕ⊥CD по теореме о трех перпендикулярах.

ΔКЕD: ∠KED = 90°, по теореме Пифагора

          KD = √(KE² + ED²) = √(9 + 9) = 3√2 м