Предмет: Алгебра,
автор: IraSt2418
Пожалуйста, помогите найти производную
Приложения:
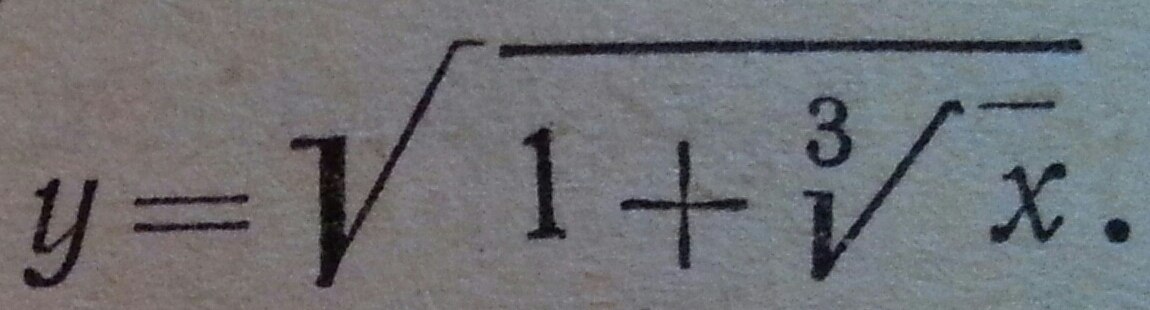
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Геометрия,
автор: liana1256
Предмет: Физика,
автор: Ipranted
Предмет: Математика,
автор: Manukovskaya