Предмет: Алгебра,
автор: Аноним
Помогите решить задания Во вложениях Задание выполните указанные действия только все расписывайте мне не нужны только ответы мне нужно решение их всего 6 примеров
Приложения:
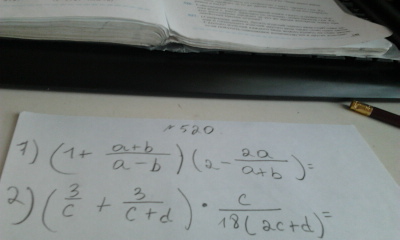


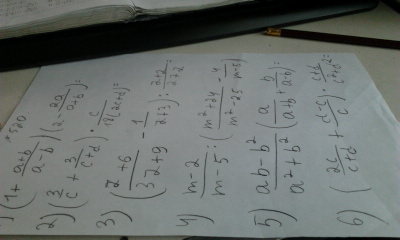
Ответы
Автор ответа:
2
Автор ответа:
2
² 5 задание там в/а+в см последний фаил
Приложения:


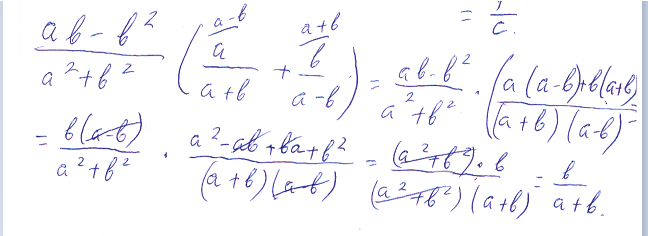
Похожие вопросы
Предмет: Русский язык,
автор: laimon9427
Предмет: Русский язык,
автор: kenankeshka
Предмет: Русский язык,
автор: KruzTV
Предмет: Математика,
автор: polinchik55
Предмет: География,
автор: kriiisper