Предмет: Алгебра,
автор: juliarimar
Помогите срочно!
Нужно с графиком решить 3 примера!
Умоляю, ставлю все свои баллы.
Очень важная домашняя работа!
задание во вложении!
Если кому то мой почерк не понятен, напишите
Спасибо огромное тем кто поможет!
Приложения:

Ответы
Автор ответа:
0
1
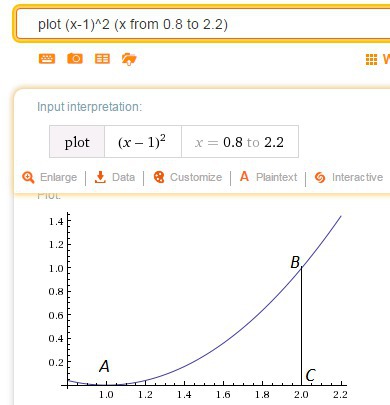
функция пересекает ось ОХ в точке с абсциссой
пересекает ось ОХ в точке с абсциссой  значит площадь, которую спросили найти в задаче, площадь криволинейного треугольника находим как:
значит площадь, которую спросили найти в задаче, площадь криволинейного треугольника находим как:


2
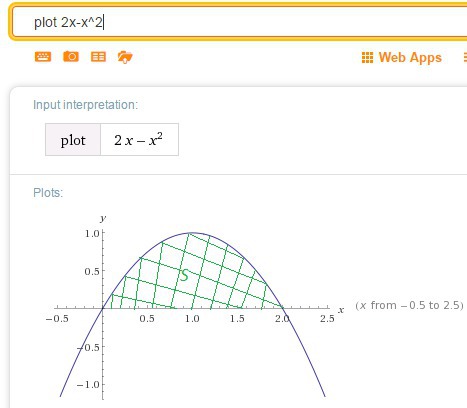
функция - парабола ветками вниз, поскольку перед
- парабола ветками вниз, поскольку перед  стоит минус
стоит минус
ищем точки пересечения этой параболой оси ОХ:



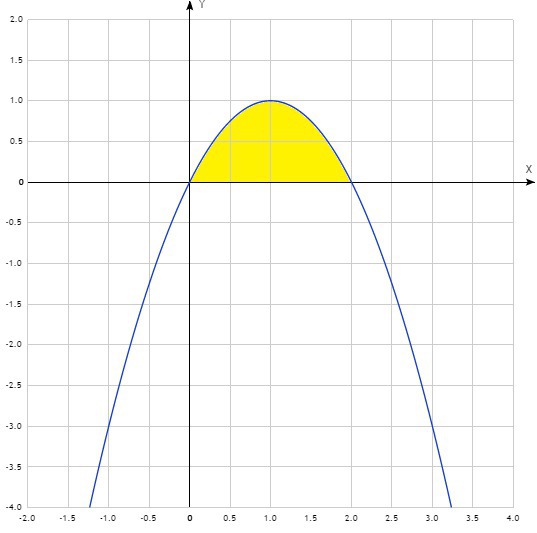
парабола пересекает ось ОХ в точках с абсциссами и
и 
вершина параболы :
:


искомая площадь:


3
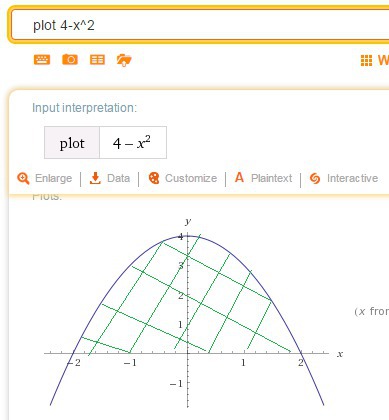
функция - парабола ветками вниз, поскольку перед
- парабола ветками вниз, поскольку перед  стоит минус
стоит минус
ищем точки пересечения этой параболой оси ОХ:



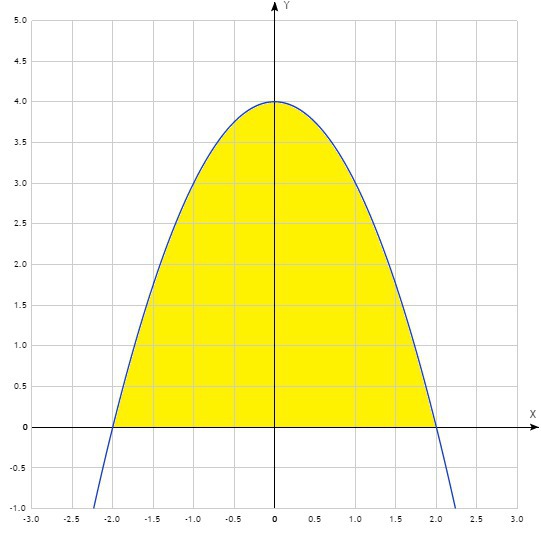
парабола пересекает ось ОХ в точках с абсциссами и
и 
вершина параболы совпадает с точкой, в которой она, парабола, пересекает ось ОУ, и это точка: , это очевидно из того факта, что выражение
, это очевидно из того факта, что выражение  принимает свое наибольшее значение
принимает свое наибольшее значение  при
при  .
.
искомая площадь:


функция
2
функция
ищем точки пересечения этой параболой оси ОХ:
парабола пересекает ось ОХ в точках с абсциссами
вершина параболы
искомая площадь:
3
функция
ищем точки пересечения этой параболой оси ОХ:
парабола пересекает ось ОХ в точках с абсциссами
вершина параболы совпадает с точкой, в которой она, парабола, пересекает ось ОУ, и это точка:
искомая площадь:
Приложения:
Автор ответа:
0
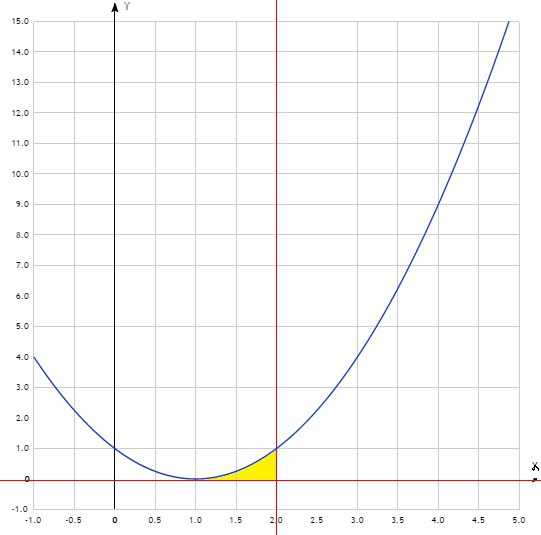
1. Чертим график и по нему определяем внешний вид искомой трапеции и пределы в которых она находится. В данном задании это 0 и 2. Так как геометрический смысл определённого интеграла это площадь, то остаётся найти этот интеграл:


2. Снова чертим график и по нему определяем пределы интегрирования, в этом задании это 0 и 2. Теперь находим интеграл

3. И опять график и пределы интегрирования: -2 и 2.


2. Снова чертим график и по нему определяем пределы интегрирования, в этом задании это 0 и 2. Теперь находим интеграл
3. И опять график и пределы интегрирования: -2 и 2.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: manukyan16
Предмет: Алгебра,
автор: Gezzhhaaa13
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: AntonSTR