Question

помогите пожалуйста:
В окружности с центром O проведен диаметр. A и B-точки окружности, расположенные по одну сторону от этого диаметра. На диаметре взята точка M такая, что AM и BM образуют равные углы с диаметром. Докажите, что угол AOB равен углу AMB.

Answer 1

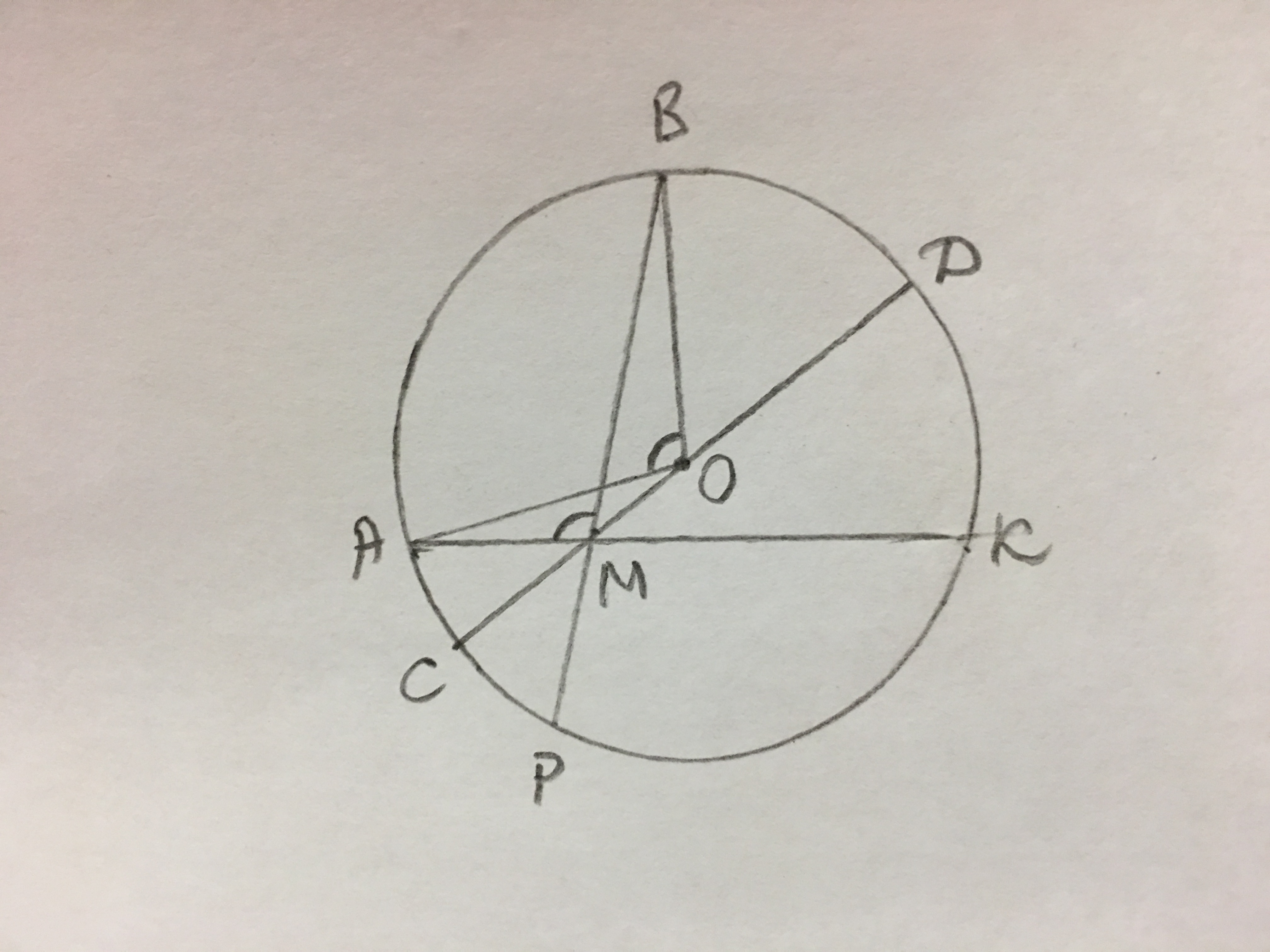
Обозначим диаметр как СД.
Продолжим прямые АМ и ВМ до второго их пересечения с окружностью в точках К и Р соответственно.
Так как ∠АМС=∠BМД по условию, ∠АМС=∠ДМК  и ∠СОР=∠ВОД 
как вертикальные, то ∠АОС=∠СОР и ∠ВОД=∠ДОК.
Диаметр СД делит окружность на две равные полуокружности, в которых есть две пары равных дуг. ∩АС=∩СР и ∩ВД=∩ДК, значит ∩АВ=∩КР.
Если точка пересечения двух секущих к окружности находится внутри окружности, то угол между секущими равен полусумме дуг, которые они высекают.
АК и ВР - секущие, М - точка их пересечения. ∠АМВ=(∩АВ+∩КР)/2=2·∩АВ/2=∩АВ.
∩АВ=∠АОВ ⇒ ∠АОВ=∠АМВ.
Доказано.