Question

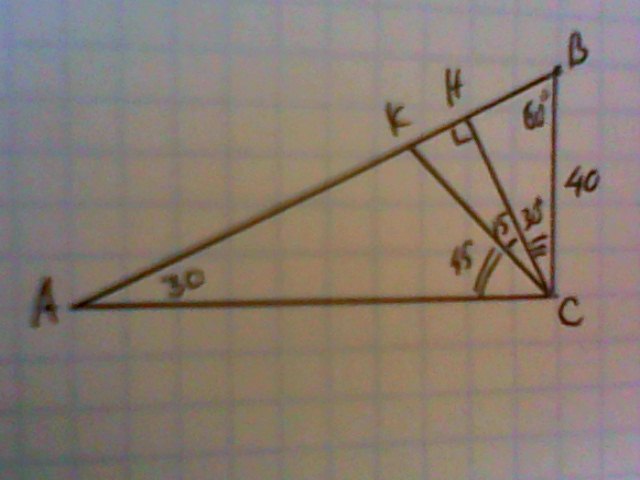
В прямоугольном треугольнике АВС угол между биссектрисой СК и высотой СН,проведенными из вершины прямого угла С,равен 15°.Сторона BC=40 см.Найдите сторону AB,если известно,что точка К лежит между A и H.

Answer 1

Биссектриса СК делит прямой угол на равные части.
∠АСК=ВСК=45°,
∠ВСН=45-15=30°.
ΔВСН - прямоугольный с острым углом 30°.ВС=2ВН.
ВН=20 см. СН²=ВС²-ВН²=1600-400=1200,
СН=√1200=20√3 см.
ΔАСН - прямоугольный с острым углом ∠САН=30°, АС=2СН=40√3.
ΔАВС: АВ²=АС²+ВС²=(40√3)²+40²=6400.
АВ=√6400=80 см.
Ответ: 80 см.