Question

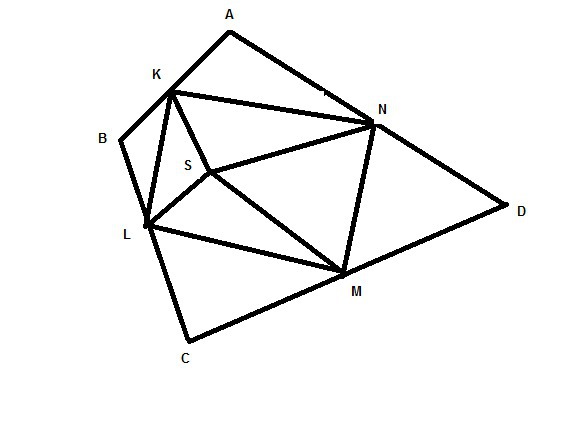
В выпуклой четырехугольнике ABCD точка К - середина АВ, точка L - середина ВС, точка М - середина СD, точка N - середина DA. Для некоторой точки S, лежащей внутри четырехугольника ABCD, оказалось, что KS=LS и NS=MS. Докажет, что угол KSN=углу MSL
Помогите, пожалуйста)

Answer 1

Для  треуг-ка АВD прямая KN является средней линией, значит она параллельна диагонали BD.  Для треуг-ка BCD отрезок LM является средней линией и он тоже параллелен диагоналиBD. Значит  KN и ML параллельны. Аналогично KLпараллельна MN. То есть KLMN это параллелограмм.  Треугольники KSN и LSM равны ( по трем сторонам), поэтому углыKSN иMSL равны

Answer 2

ПЫТАЮСЬ отправить чертеж...

Answer 3

Спасибо большое. Но у меня вопрос, можно ведь доказать, что углы KSN=MSL, потому что они вертикальны?

Answer 4

это частный случай, когда S на пересечении диагоналей.....они не обязаны быть вертикальными... потому что точка s может располагаться не только на диагонали