Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, решить.
Приложения:
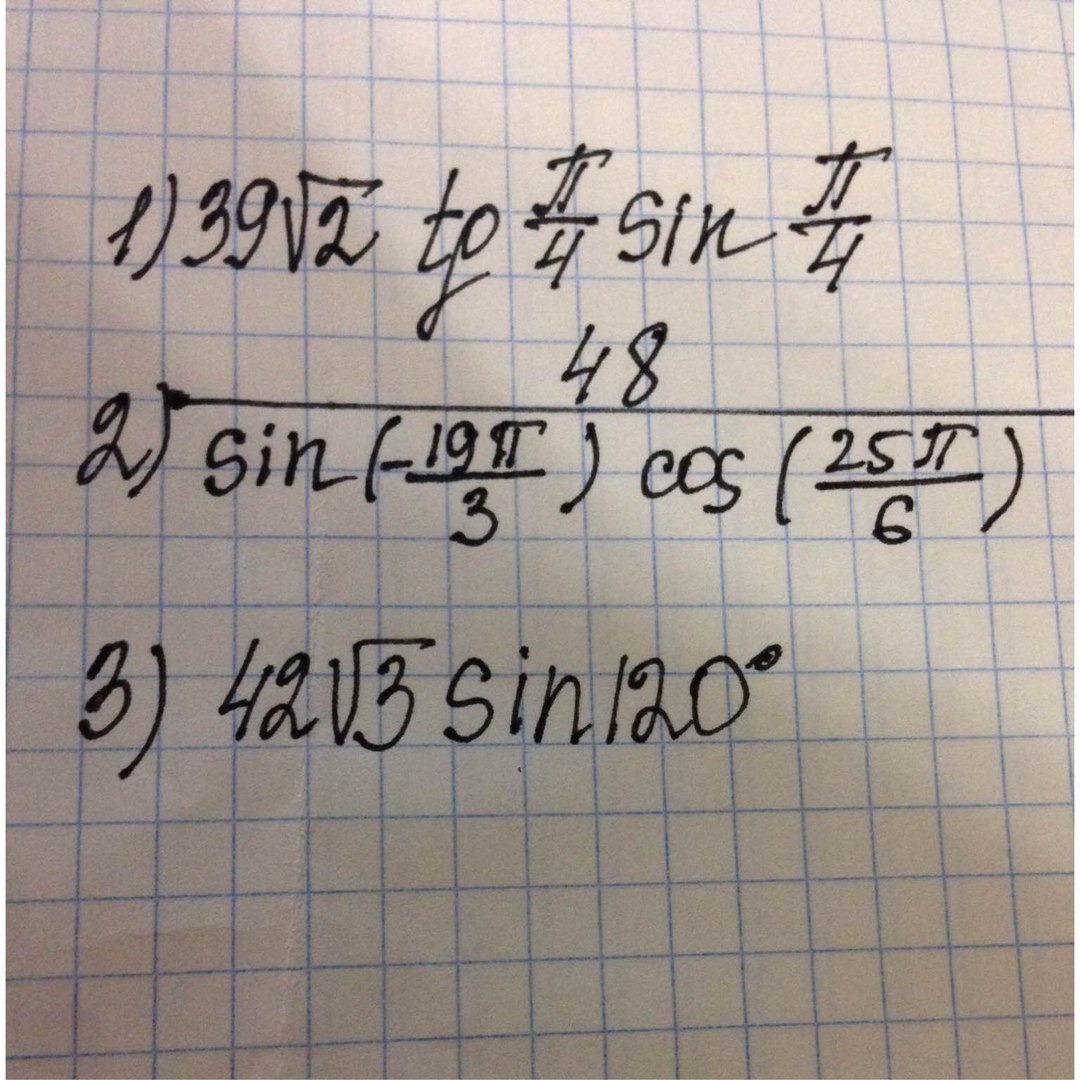
Ответы
Автор ответа:
0
1) 

2)


3)

2)
3)
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: nazgerbog
Предмет: Биология,
автор: Nata23er
Предмет: Математика,
автор: aljan2005