Предмет: Геометрия,
автор: ksutigra
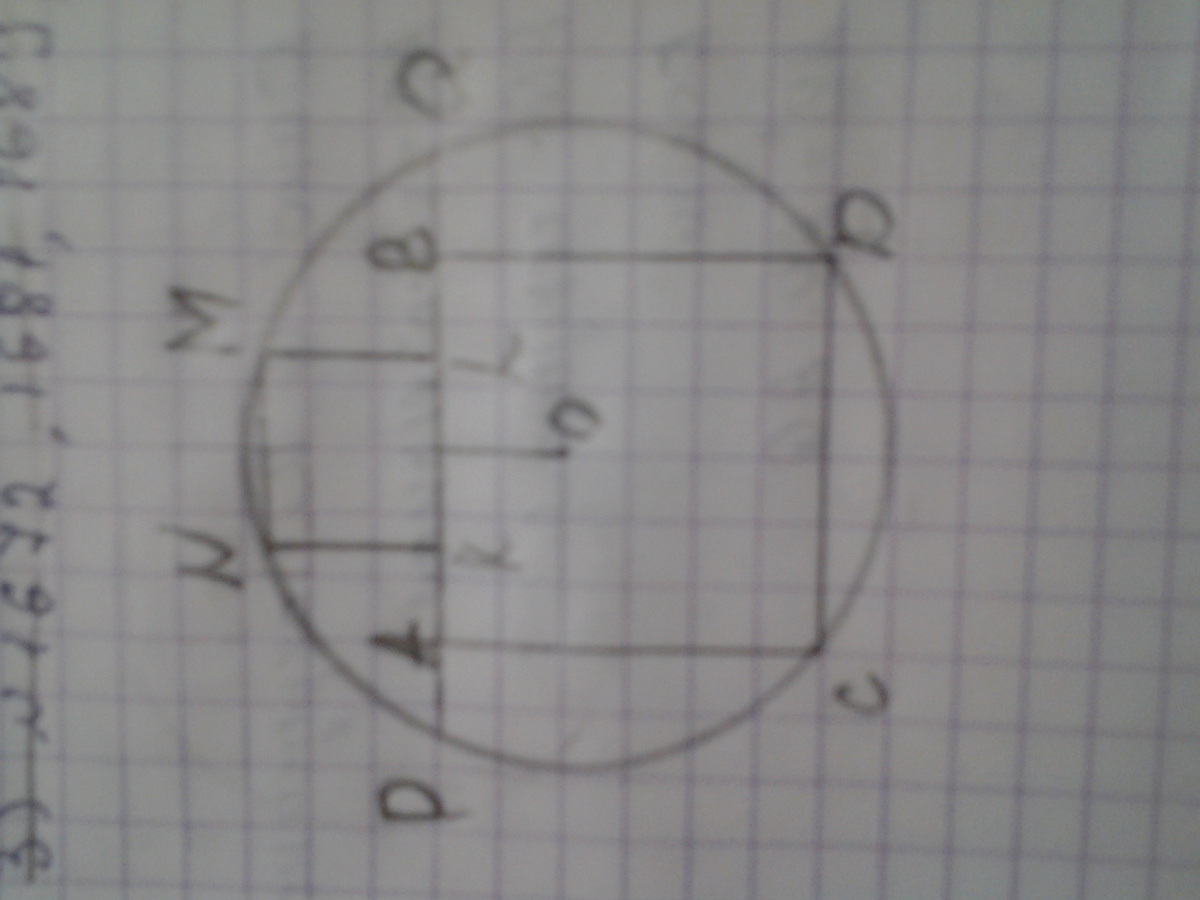
Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, две другие-на хорде. Чему равна разность длин сторон квадрата? Я смотрела здесь и все равно не поняла ( а нам это еще и объяснять... нельзя ли как нибудь непонятнее?
Приложения:

Ответы
Автор ответа:
29
Обозначим длины сторон большого и малого квадратов через 2х и 2у соответственно, радиус окружности – через R. Тогда расстояния от центра окружности до вершин вписанных квадратов, лежащих на окружности дают выражения
(2х – h)^2 + x^2 = R^2
(2y + h)^2 + y^2 = R^2
Приравняем левые части выражений, упростим.
В результате получим x - y = (4/5)h.
Тогда, разность длин сторон квадратов (т.е. 2х - 2у) будет равна (8/5)h.
^2 - это "в квадрате", т.е например x^2 - это икс в квадрате
Похожие вопросы
Предмет: Русский язык,
автор: bossshkirmontomar
Предмет: Русский язык,
автор: tnechaeva054
Предмет: Қазақ тiлi,
автор: KarinaMedeuova06
Предмет: Математика,
автор: dayana070619456
Предмет: Химия,
автор: Katyaanto