Question

BM - медиана треугольника ABC, O - произвольная точка пространства. Разложите вектор BM по векторам OA=a OB=b OC=c.

С рисунком!!! В paint-е заделайте,плиз.

Answer 1

Правило: "Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое)".
В нашем случае (все вектора):
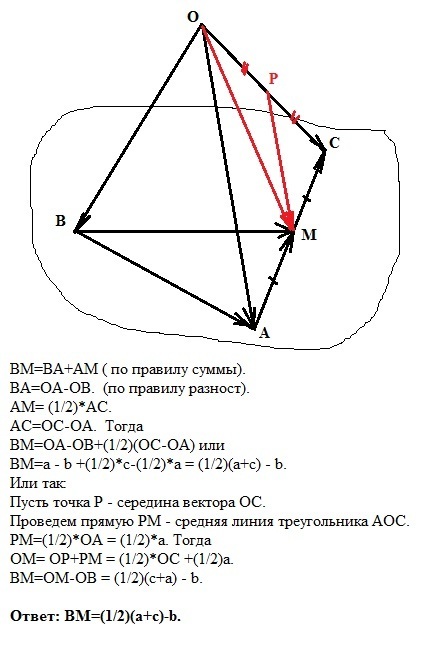
ВМ=ВА+АМ ( по правилу суммы).
ВА=ОА-ОВ (по правилу разности).
АМ= (1/2)*АС.
АС=ОС-ОА.  Тогда
ВМ=ОА-ОВ+(1/2)(ОС-ОА) или
ВМ=а - b +(1/2)*c-(1/2)*a = (1/2)(a+c) - b.
Ответ: ВМ=(1/2)(a+c)-b.

Или так:
Пусть точка Р - середина вектора ОС.
Проведем прямую РМ - средняя линия треугольника АОС.
РМ=(1/2)*ОА = (1/2)*а. Тогда
ОМ= ОР+РМ = (1/2)*ОС +(1/2)а.
ВМ=ОМ-ОВ = (1/2)(с+а) - b.
Ответ: ВМ=(1/2)(a+c)-b.