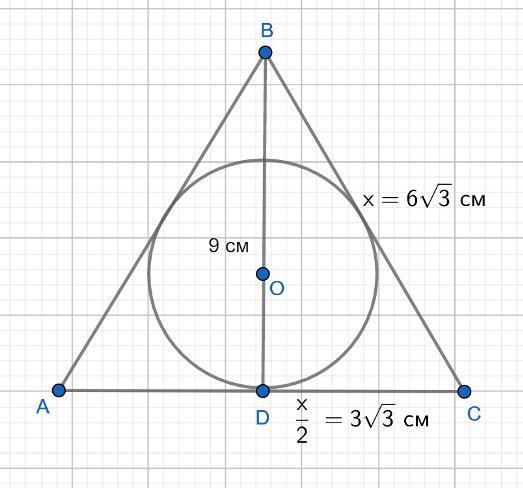
Высота равностороннего треугольника равна 9 см. Найдите длину окружности, вписанной в этот треугольник.
A) 20π
B) 4,5π
C)9π
D)6π
Ответы
Ответ:
D) 6π
Пошаговое объяснение:
Длина окружности C = 2πr;
Радиус вписанной окружности r = S/p (S - площадь треугольника, p - полупериметр треугольника).
1) Найдем сторону ΔABC.
Обозначим сторону ΔABC через x. Высота в равностороннем треугольнике является биссектрисой и медианой. Отрезок DC = 1/2 стороны AC = x/2.
По т.Пифагора из ΔDBC найдем x:
9² = x² - x²/4; 81 = 3x²/4; x² = 4*81/3; x = 2*9/√3 = 18*√3/3 = 6√3;
Сторона ΔABC = 6√3;
2) Полупериметр ΔABC: p = 3*6√3/2 = 9√3;
3) Площадь ΔABC: S = 1/2 * a * h = 1/2 * 6√3 * 9 = 27√3;
4) Радиус вписанной в треугольник окружности:
r = S/p = 27√3 / 9√3 = 3 (см);
5) Длина окружности: C = 2πr = 2π*3 = 6π (см).
Длина окружности: C = 6π см.
Ответ D) 6π.
Ответ:
D) 6П
Пошаговое объяснение:
Центр вписанной и описанной окружности в равностороннем треугольнике находится в точке пересечения медиан (они же высоты и биссектрисы).
Эта точка делит высоты в отношении 1:2.
Это значит, что радиус вписанной окружности равен 1/3 высоты.
А радиус описанной окружности равен 2/3 высоты.
Итак, радиус r = h/3 = 9/3 = 3 см.
Длина окружности равна C = 2П*r = 2П*3 = 6П
