Помогите с задачкой..ABCD - квадрат со стороной, равной 4 см. Треугольник АМВ имеет общую сторону АВ с квадратом, АМ= ВМ= 2 см. Плоскости треугольника и квадрата взаимно перпендикулярны.
1) Докажите, что ВС ┴ AM.
2) Найдите угол между МС и плоскостью квадрата.
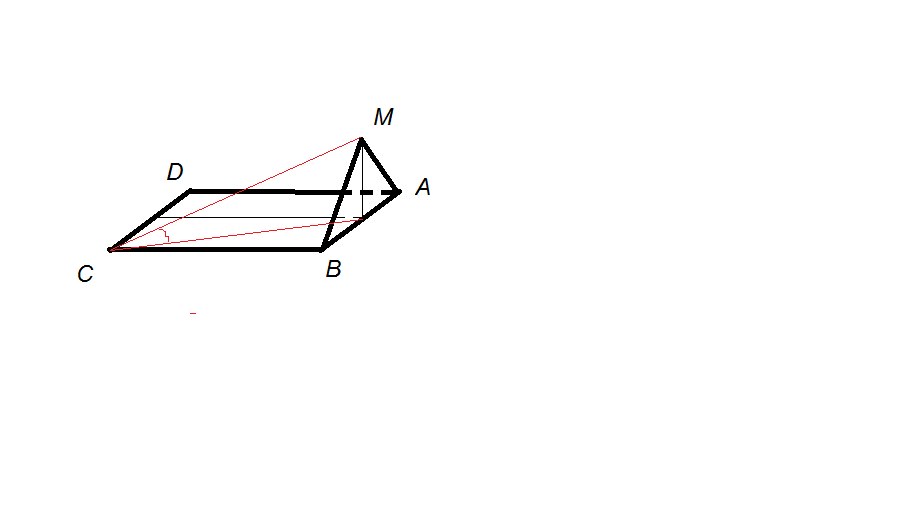
Ответы
1) если две плоскости _|_ и в одной из них провести _|_ к их линии пересечения, то этот перпендикуляр будет перпендикулярен ВСЕЙ второй плоскости (т.е. любой прямой, лежащей в другой плоскости)
т.е. если в плоскости квадрата прямая (СВ, DA) _|_ АВ, то она _|_ и любой прямой из плоскости треугольника
АВ и СВ (АВ и DA) перпендикулярны (как стороны квадрата) => и СВ и DA _|_ любой прямой, лежащей в плоскости треугольника: CB _|_ MB, CB _|_ MA, DA _|_ MB, DA _|_ MA...
2) треугольник BMA равнобедренный, высота МК будет и медианой, => BK=AK=AB/2 = 2
MK^2 = MA^2 - AK^2 = MA^2 - 4 (в условии, видимо, опечатка... МА не может быть =2...)
СК^2 = CB^2 + BK^2 = 4^2 + 2^2 = 16+4 = 20
CK = корень(20) = 2корень(5)
угол MCK можно найти по определению любой тригонометрической функции...
sin(MCK) = MK / CM
cos(MCK) = CK / CM
CM^2 = CK^2 + MK^2
tg(MCK) = MK / CK = MK / (2корень(5))