Question

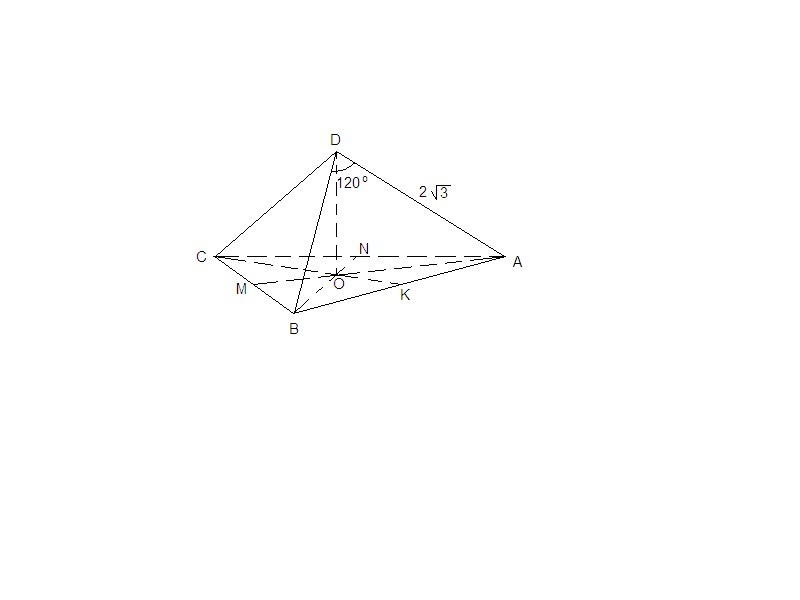
DABC- Правильная пирамида. DO перпендикулярна(ABC), CK перпендикулярна AB, AMперпендикулярна BC, BM перпендикулярна AC. AD=2 корень из 3, угол ADB= 120 градусов. Надо найти P основания.

Answer 1

Так как пирамида правильная, в основании лежит правильный треугольник, боковые грани - равные равнобедренные треугольники.

DA = DB = DC = 2√3.

Из ΔDAB по теореме косинусов:

АВ² = DA² + DB² - 2·DA·DB·cos120°

AB² = (2√3)² + (2√3)² - 2 · 2√3 ·2√3 · (- 1/2)

AB² = 12 + 12 + 12 = 36

AB = 6

Pabc = 3 · AB = 3 · 6 = 18