Question

ПОмОГИТЕ с ГЕОМЕТРИЕЙ!
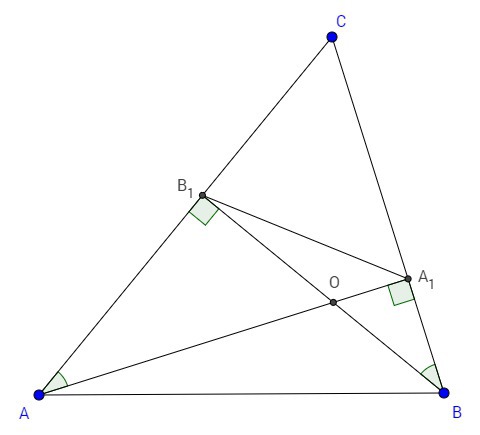
В остроугольном треугольнике АВС проведены высоты АА1 и ВВ1. Докажите, что треугольник АВС подобен треугольнику А1В1С

Answer 1

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

△AOB₁ и △A₁OB подобны
(∠AOB₁=∠A₁OB - вертикальные углы, ∠AB₁O=∠BA₁O=90)
∠B₁AO=∠A₁BO
△CAA₁и △CBB₁ подобны (∠AA₁C=∠BB₁C=90)
B₁C/A₁C = BC/AC <=> B₁C/BC = A₁C/AC

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

△ABC и △A₁B₁C подобны (∠ACB - общий)

Answer 2

спасибо большое