помогите с тремя заданиями и распишите все решение.
Ответы
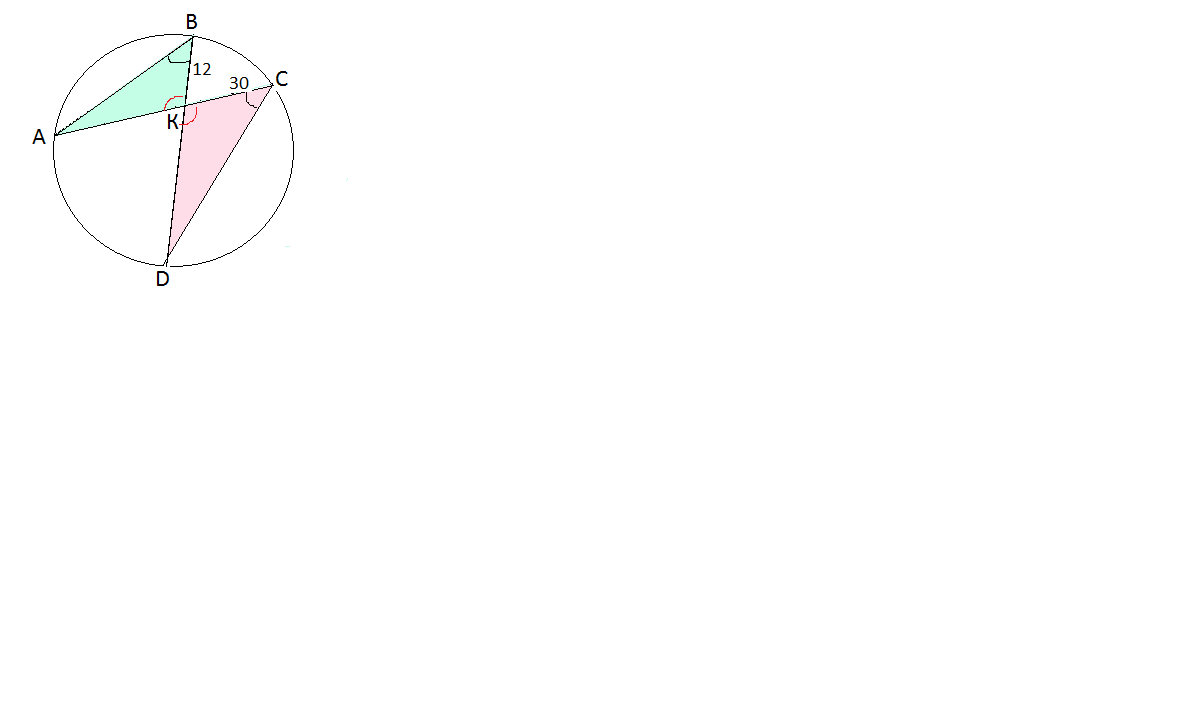
1)
Углы В и С опираются на одну дугу и потому равны.
Углы при К равны как вертикальные.
Треугольники АВK и CKD подобны по равным углам.
Коэффициент подобия 2/5
В подобных треугольниках отношение периметров равно отношению их сторон.
РΔ АКВ: Р CKD =2:5
28: Р CKD =2:5
2 Р CKD= 140 см
Р Δ CKD=70 см
-------------
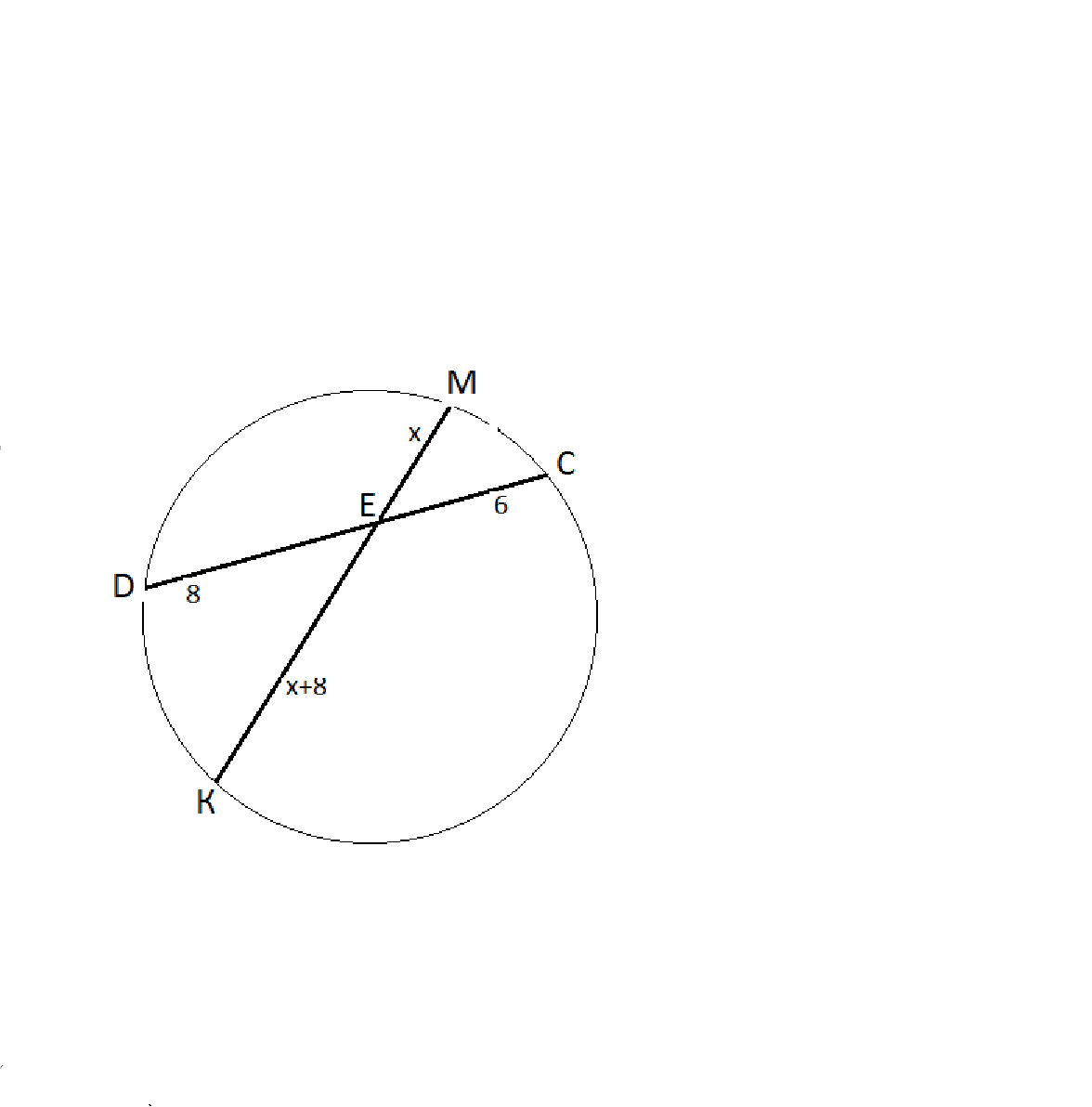
2)
Произведение отрезков пересекающихся хорд равно.
СЕ·ЕД=КЕ·ЕМ
6·8=(х+8)х
х²+8х-48=0
Решив квадратное уравнение, находим его корни.
х₁=4
х₂ = -12 ( не подходит, длина - величина положительная))
КМ=КЕ+ЕМ=х+х+8
КМ=16
Проверка:
СЕ· ЕД=КЕ·ЕМ
6·8=4·12=48
--------------------
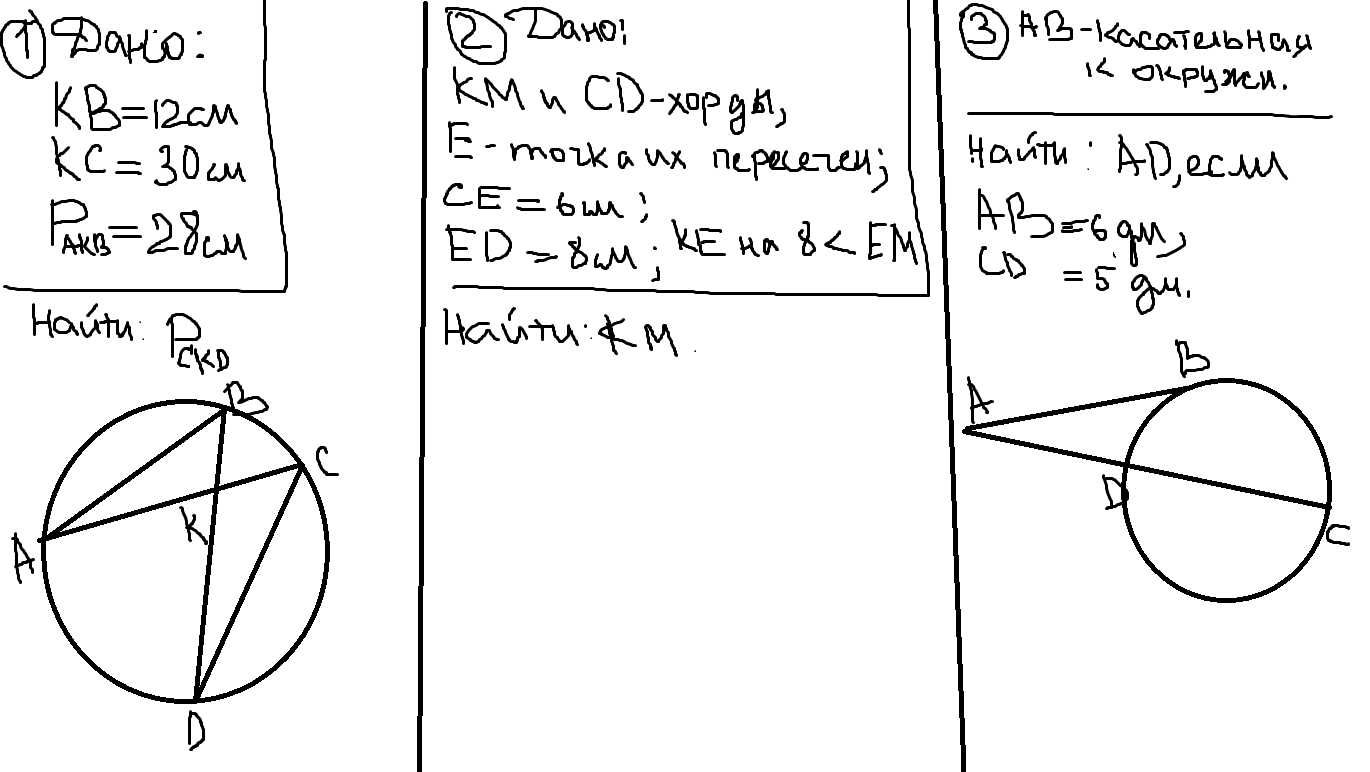
3)
Если из точки (А) вне окружности к ней проведены касательная и секущая, то
квадрат длины отрезка (АВ )касательной равен произведению всего отрезка (АС) секущей на его внешнюю часть (АD).
АВ²=АС·АD
Пусть АD=х
Тогда АС=х+5
АВ²=АС·АD
36=х(х+5)
х ²+5х-36=0
Решив квадратное уравение, получим
х₁=4
х₂= -9 ( не подходит)
АD=4