Question

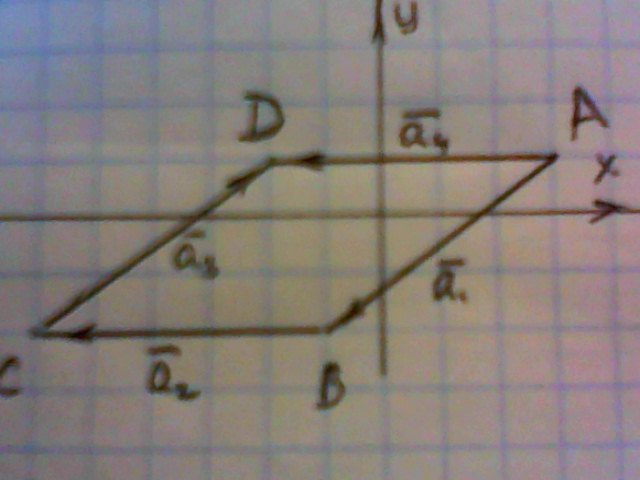
Четырехугольник образован векторами а1, а2, а3, а4, при чем а1=AB, а2=BC, a3=CD, а a4=a1+a2+a3. Нарисуйте полученный четырехугольник, определите его вид и площадь.
Координаты точек A, B, C, D равны:
А=(3;1) В=(-1;-2) С=(-6;-2) D=(-2;1)

Answer 1

Определим координаты векторов и их абсолютную величину (длину)
АВ(-4; -3), |АВ|=√(-4)²+(-3)² =5,
ВС(-5; 0), |ВС|=√(-5)²+0² =5,
СD(4; 3), |СD|=√4²+3² =5,
АD(-5; 0), |АD|=√(-5)²+0² =5,
АСВD- ромб,
его площадь S=5·3=15. Высота равна 3, сторона 5.
Ответ: ромб. 15 кв. ед.

Answer 2

Спасибо огромное, очень выручили :з