Предмет: Алгебра,
автор: Артур998
f(x) = x³ – 2x² + x . Решить по этому плану .
Приложения:




Ответы
Автор ответа:
0
1. Область определения функции - все действительные числа:
2. Исследование функции на четность:
Функция ни четная, ни нечетная (общего вида)
3. Точки пересечения с осями координат:
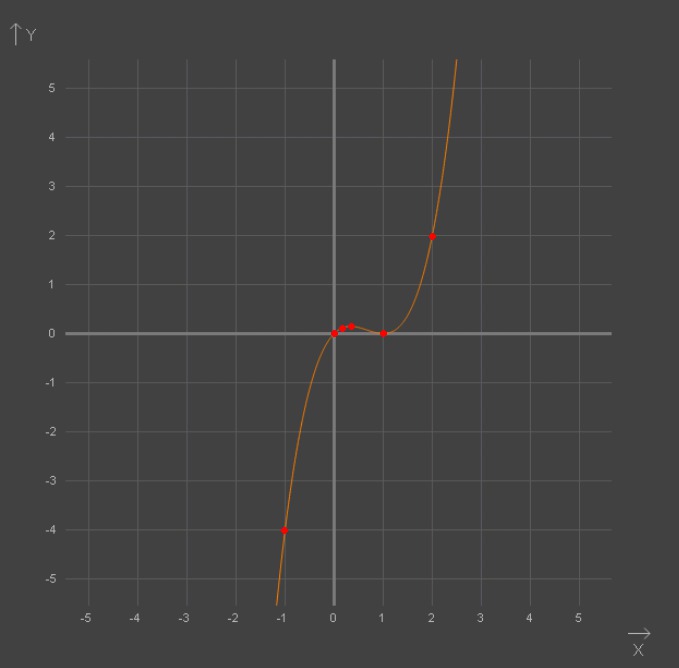
Точки пересечения с осью х: (0; 0); (1; 0)
Точка пересечения с осью y: (0; 0)
4. Исследование функции на монотонность и экстремумы:
Точка максимума:
Точка минимума:
При
При
5. Исследование функции на выпуклость/вогнутость:
Точка перегиба:
Ордината точки перегиба:
При
При
6. Построение графика:
Имеющиеся точки: (0; 0); (1; 0); (1/3; 4/27); (2/3; 2/27)
Просчитаем еще пару точек для определения крутизны графика:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: alenaalena24150
Предмет: Русский язык,
автор: arinamobil6
Предмет: Русский язык,
автор: fuzzybv
Предмет: Математика,
автор: puchkova20032
Предмет: Информатика,
автор: pakkristy