Предмет: Алгебра,
автор: InterSphere
Дифференциальные уравнения
Приложения:
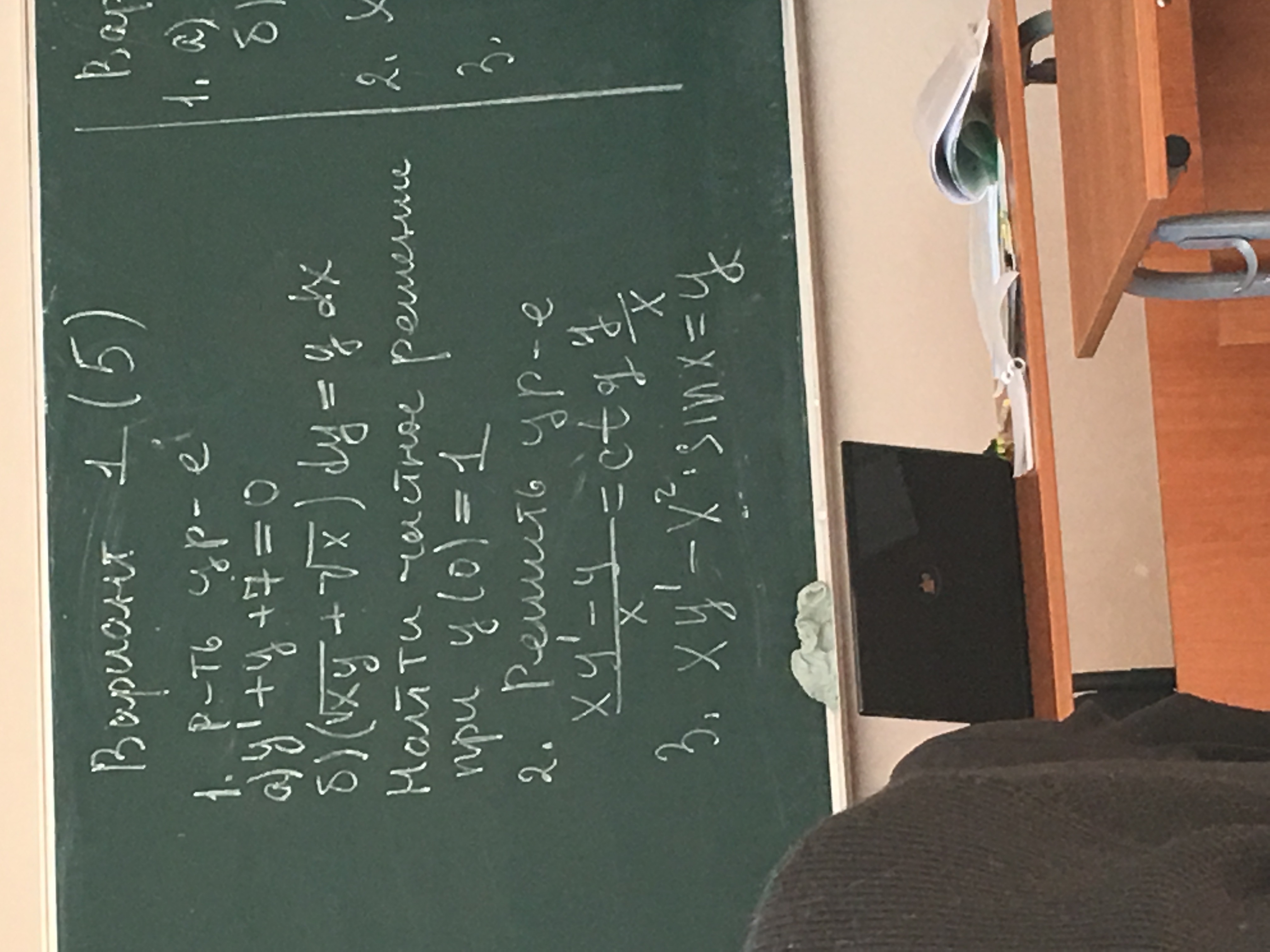
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Химия,
автор: ann40695
Предмет: Українська мова,
автор: vikakrystan
Предмет: Литература,
автор: lisalicean83
Предмет: Математика,
автор: Mini127
Предмет: Физика,
автор: valeriyapalamar