Предмет: Математика,
автор: meizu19
помогите решить, пожалуйста .
Вычислите площадь фигуры ограниченной лиеями.
у=2х^2, у=0. х=2
Ответы
Автор ответа:
0
С точки зрения геометрии определённый интеграл это площадь.

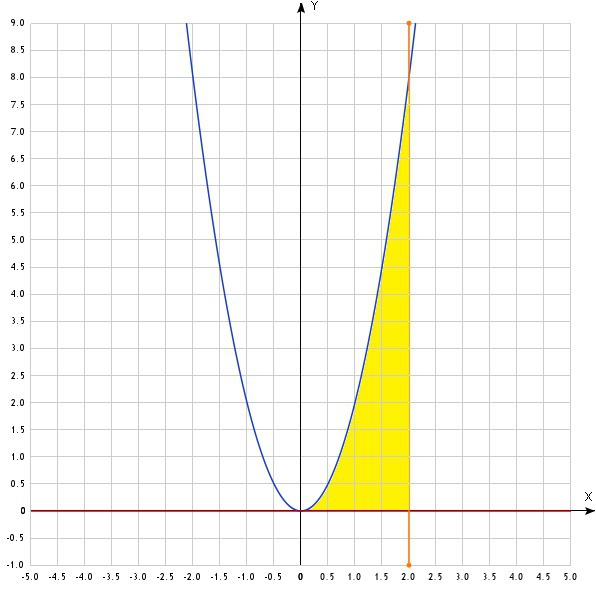
Чертим рисунок, по которому определяем площадь какой фигуры необходимо найти (обозначена жёлтым цветом), и пределы интегрирования. В нашем примере фигура ограничена на отрезке [0;2], график функции 2х² лежит над осью ОХ, поэтому
 ед².
ед².
Чертим рисунок, по которому определяем площадь какой фигуры необходимо найти (обозначена жёлтым цветом), и пределы интегрирования. В нашем примере фигура ограничена на отрезке [0;2], график функции 2х² лежит над осью ОХ, поэтому
Приложения:
Похожие вопросы
Предмет: Физика,
автор: SOSOKPISOSA1337
Предмет: Другие предметы,
автор: Аноним
Предмет: Физика,
автор: MadDino
Предмет: Физика,
автор: vovamanak1
Предмет: Физика,
автор: Пе4енюФФко