Question

Помогите , пожалуйста

Answer 1

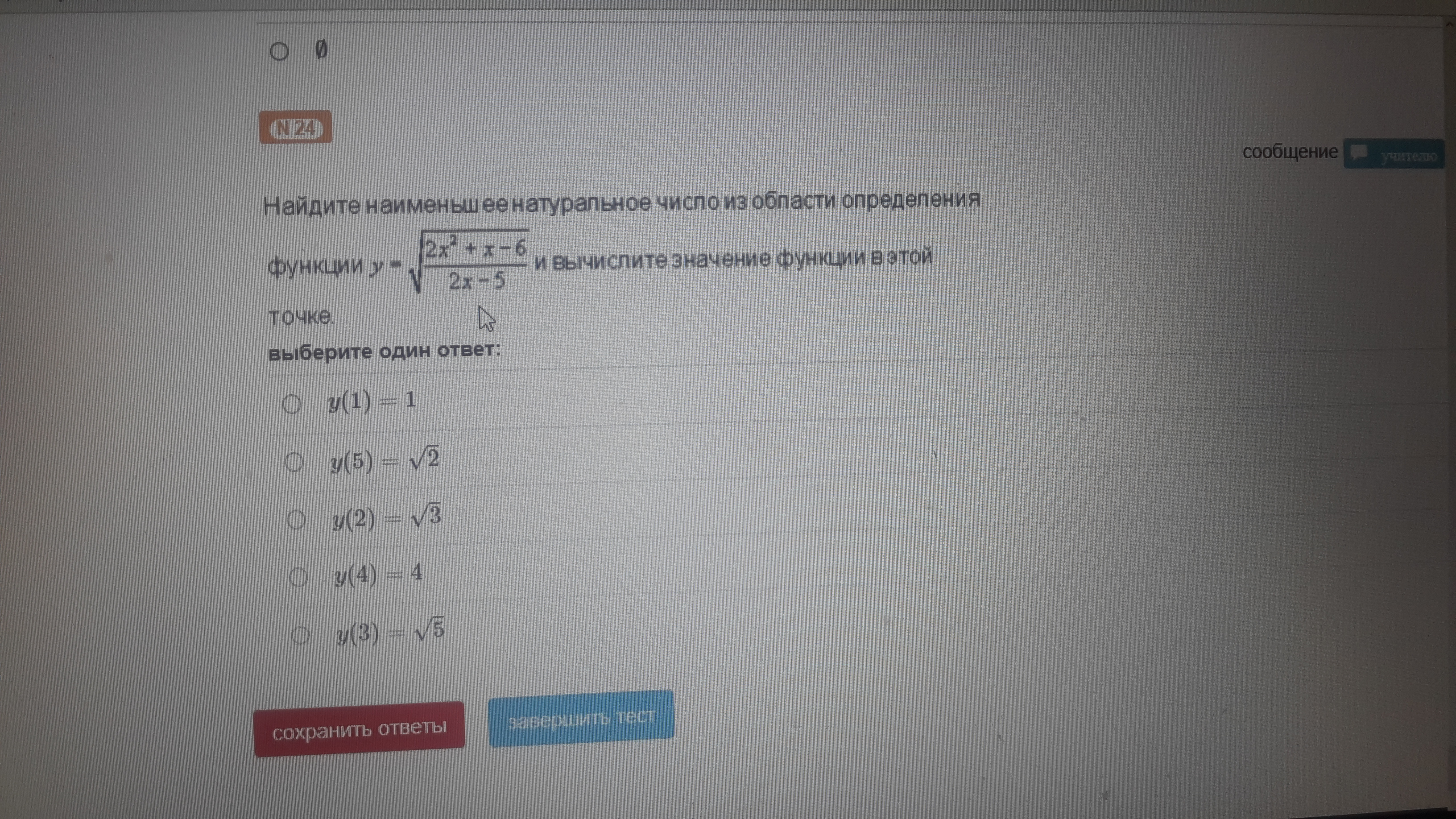
x≠2,5  ;  (2x²+x-6)/(2x-5)≥0  ⇔[(2x - 3)(x+2)]/(2x -5)≥0
  1)  2x-3≥0      ; x+2≥0  ; 2x -5 >0   ⇒  
          x ≥ 1,5    ; x ≥ -2   ;  x > 2,5     ⇔  x >2,5

   2)  2x-3≥0     ; x+2≤0  ; 2x -5 <0   ⇒
          x ≥ 1,5    ;  x≤ -2   ;   x<2,5        ⇔  x = ∅
    3)  2x-3≤0    ; x+2≥0  ;  2x - 5<0  ⇒
          x≤1,5      ; x≥-2     ;   x<2,5        ⇔  x ∈[ -2; 1,5]
     4) x≤ 1,5      ; x≤-2    ;   x>2,5         ⇔ x = ∅
             ⇒  x ∈ [ -2 ; 1,5] U (2,5 ; ∞)

a)  y(1) = √[(2+1-6)/(2-5)]= 1      верно
b)  y(5) = √ 49/5  ≠√2
c)   2 ∉  [ -2 ; 1,5] U (2,5 ; ∞)
d)  y(4) =√30/3 ≠ 4
e)  y(3) = √16/1 = 4 ≠ √5