Предмет: Алгебра,
автор: Аноним
номер 54 пожалуйста!!!!!!!
Приложения:

Ответы
Автор ответа:
0
Формула сosα·sinα=sin2α/2
Формула 2cos²α=1+cos2α
Приложения:
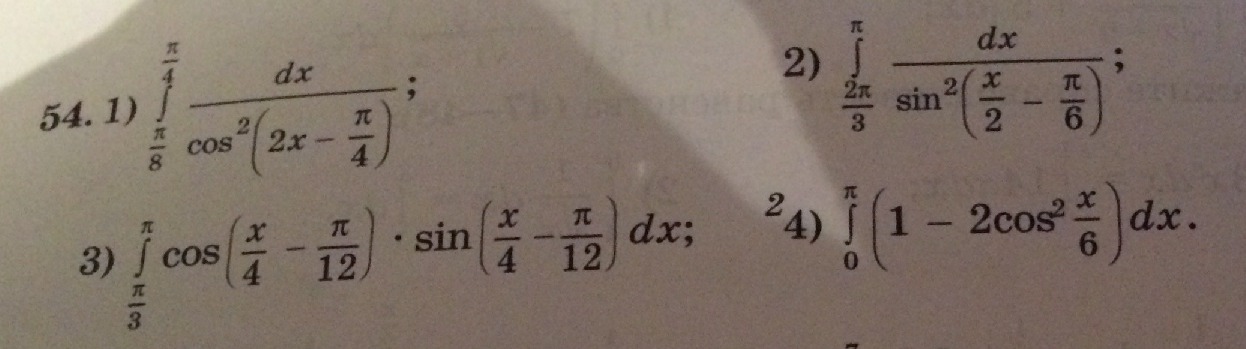
Похожие вопросы
Предмет: Русский язык,
автор: s0660572734
Предмет: Алгебра,
автор: 87867123
Предмет: Математика,
автор: younormal228
Предмет: Биология,
автор: Ledinko